Основы работы с Python: инструментарий на Python для решения научных и прикладных задач

Инструментарий для научной визуализации

Построения графиков функций с библиотекой Matplotlib

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import ipywidgets as widgets
from ipywidgets import interact, interact_manual, Label
import seaborn as sns
sns.set()
sns.set(style="whitegrid")

%matplotlib inline

A = 1
omega = 1


def f_sin(t, A, omega):
    ''' Определяет значение функции A*sin(omega*t),
        A, omega - параметры'''
    return (A*np.sin(omega*t))

print(f_sin.__doc__)

 Определяет значение функции A*sin(omega*t),
        A, omega - параметры

Массивы в numpy

# Массив чисел: линейная последовательность с 0 по 30 с шагом 2

x = np.arange(0, 30, 2)
print(x)

[ 0  2  4  6  8 10 12 14 16 18 20 22 24 26 28]

Еще один способ задания массива См. ссылку. :

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)[source]
Return evenly spaced numbers over a specified interval.

Returns num evenly spaced samples, calculated over the interval [start, stop].

The endpoint of the interval can optionally be excluded.

x2 = np.linspace(0, 30, 20, endpoint=True)
print(x2)
print(x2.shape)

[ 0.          1.57894737  3.15789474  4.73684211  6.31578947  7.89473684
  9.47368421 11.05263158 12.63157895 14.21052632 15.78947368 17.36842105
 18.94736842 20.52631579 22.10526316 23.68421053 25.26315789 26.84210526
 28.42105263 30.        ]
(20,)

t = np.linspace(-4*np.pi, 4*np.pi, 150, endpoint=True)

print(t.shape)

(150,)

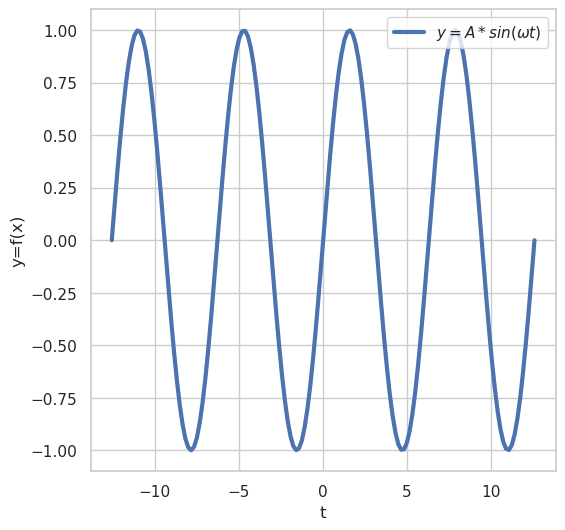
fig = plt.figure(figsize=(6, 6))
plt.plot(t, f_sin(t, A, omega), label='$y=A*sin(\\omega t )$', linewidth=3.0)
plt.xlabel('t', size=12)
plt.ylabel('y=f(x)', size=12)
plt.legend(loc='upper right')
plt.show()

Интерактивное управление в Jupyter Notebooks: библиотека IPywidgets

Для решения задач интерактивного управления параметрами воспользуемся библиотекой IPywidgets (См. ссылку). С помощью этой библиотеки блокнот Jupyter превращается в диалоговую панель, удобную для визуализации и работы с данными (больше о возможностях, предоставляемых библиотекой, см статью Интерактивное управление в Jupyter Notebooks).

Для работа с IPywidgets создаем ячейку с :

import ipywidgets as widgets
from ipywidgets import interact, interact_manual, Label

Список доступных виджетов (Widget List) можно найти на сайте библиотеки.

Однако, в библиотеке есть удобная функция (ipywidgets.interact), котороя автоматически создает элементы управления пользовательского интерфейса (UI) для интерактивного изучения кода и данных. Это самый простой способ начать использовать виджеты IPython. Мы воспользуемся конструкцией (декоратор):

                                                                          
@interact 

которая автоматически создаёт и текстовое поле и слайдер для выбора колонки и числа. Декоратор смотрит на введённые параметры и создаёт панель диалогового управления, основываясь на типах данных. Пример

%matplotlib widget 

@interact(t=1.0, A=1, omega=1)
def f_sin(t, A, omega):
    ''' Определяет значение функции A*sin(omega*t),
        A, omega - параметры'''
    return A*np.sin(omega*t)

Некоторые улучшения Sliders

Добавим для слайдеров интервалы и шаг изменения. Пример:

@interact(x=(0.0, 20.0, 0.5))
def h(x=5.5):
    return x

Для нашей задачи определим функцию, с интерактивными всеми параметрами (амплитуда и частота):

@interact
def show_sin(A=1, omega=1):
    t = np.linspace(-4*np.pi, 4*np.pi, 150, endpoint=True)
    fig = plt.figure(figsize=(6, 6))
    plt.plot(t, f_sin(t, A, omega),
             label='$y=A*sin(\\omega_t )$', linewidth=3.0)
    plt.xlabel('t')
    plt.ylabel('y=f(x)')
    plt.legend(loc='upper right')
    plt.show()

@interact
def show_sin(A=(1.0, 5.0, 1.0), omega=(0.1, 5.0, 0.1)):
    t = np.linspace(-4*np.pi, 4*np.pi, 150, endpoint=True)
    fig = plt.figure(figsize=(6, 6))
    plt.plot(t, f_sin(t, A, omega),
             label='$y=A*sin(\\omega_t )$', linewidth=3.0)
    plt.xlabel('t')
    plt.ylabel('y=f(x)')
    plt.legend(loc='upper right')
    plt.show()