Численное решение задачи Коши: библиотека SciPy

Материалы этой части основаны на книге (JBoook):

Qingkai Kong, Timmy Siauw, Alexandre M. Bayen. «Python Programming And Numerical Methods: A Guide For Engineers And Scientists»: https://pythonnumericalmethods.berkeley.edu/notebooks/Index.html

Задача Коши: Рассмотрим решение начальной задачи (Intial value problem) для сисетемы обыкновенных дифференциальных уравнений первого порядка, разрешенных ошносительно производной:

\[\begin{split} \begin{eqnarray} \begin{cases} \frac{dy(t)}{dt} = f(t,y(t)),\\ y|_{t=t_0} = y_0, \end{cases} \label{eq1} \tag{1} \end{eqnarray} \end{split}\]

где \( y=(y_1,...,y_n)^T \) - вектор-функция.

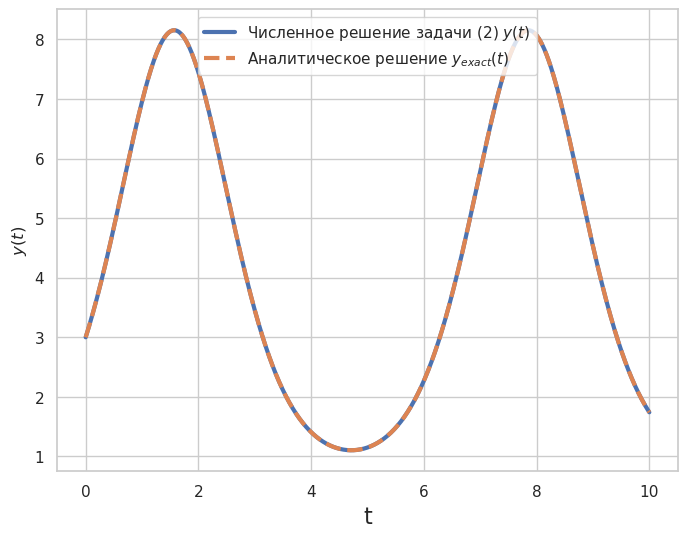
Пример 1: Численно решить задачу Коши:

\[\begin{split} \begin{eqnarray} \begin{cases} \frac{dy}{dt} = y\cos(t), \\ y(0)=y_0. \label{eq2} \tag{2} \end{cases} \end{eqnarray} \end{split}\]

Для сравнения приведем аналитическое решение задачи (2):

\[ y_{exact} = y_0 e^{sin(t)}. \]

Воспользуемся библиотекой SciPy, содержащей функцию для решения начальной задачи:

scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False, events=None, vectorized=False, args=None, **options)[source]
Solve an initial value problem for a system of ODEs.

Для этого необходимо задать правые части уравнений (2).

%matplotlib inline 

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from functools import partial
import seaborn as sns
sns.set()
sns.set(style="whitegrid")

def F_right(t, y):
    ''' Определяет правую часть ДУ,
        примера 1'''
    return y*np.cos(t)

# Параметры численного счета
t0 = 0
tf = 10
nt = 1000
# Массив точек (сетка) в которых будет находится решение
t_e = np.linspace(t0, tf, nt)
# Начальное условие
y0 = np.array([3])

def y_exact(y0, t):
    ''' Определяет точное решение ДУ,
        примера 1'''
    return y0*np.exp(np.sin(t))

# Численное решение
sol_1 = solve_ivp(F_right, [t0, tf], y0, t_eval=t_e,
                  method='RK45', rtol=1e-8, atol=1e-8)

plt.figure(figsize=(8, 6))
plt.plot(sol_1.t, sol_1.y[0], label='Численное решение задачи (2) $y(t)$',
         linewidth=3.0)
plt.plot(t_e, y_exact(y0, t_e), label='Аналитическое решение $y_{exact}(t)$',
         linestyle='--', linewidth=3.0)
plt.xlabel('t', size=16)
plt.ylabel('$y(t)$', size=12)
plt.legend(loc='upper center', fontsize=11)
plt.show()

plt.figure(figsize=(8, 6))
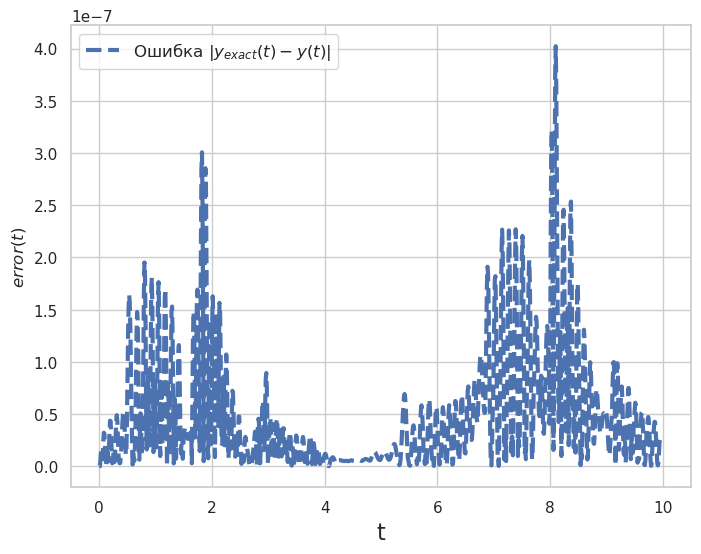
plt.plot(t_e, np.abs(y_exact(y0, t_e)-sol_1.y[0]),
         label='Ошибка $|y_{exact}(t) - y(t)|$', linestyle='--', linewidth=3.0)
plt.xlabel('t', size=16)
plt.ylabel('$error(t)$', size=12)
plt.legend(fontsize=12)
plt.show()

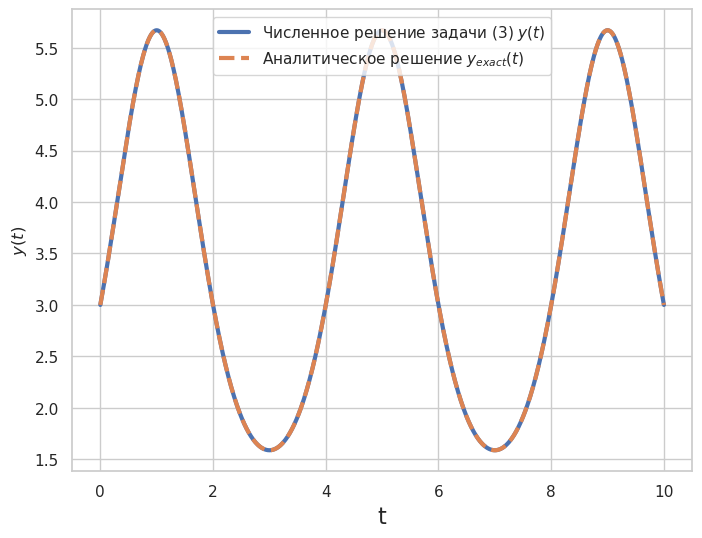
Пример 2: Численно решить задачу Коши:

\[\begin{split} \begin{eqnarray} \begin{cases} \frac{dy}{dt} = y\cos(\omega t), \\ y(0)=y_0. \end{cases} \label{eq3} \tag{3} \end{eqnarray} \end{split}\]

Для сравнения приведем аналитическое решение задачи (3):

\[ y_{exact} = y_0 e^{\frac{1}{\omega}sin(\omega t)}. \]

Отметим, что в модель входит параметр \(\omega\). Для корректной передачи параметра в функцию SciPy воспользуемся методом:

from functools import partial

Модуль functools предназначен для функций высшего порядка: функций, которые воздействуют на другие функции или возвращают их. Для решения задачи:

• Зададим правые части уравнений (3);

• “Обернем” вызов решателя с помощью функции partial, для частичного применения функции, которое «замораживает» некоторую часть аргументов функции и/или ключевых слов.

def F_right2(t, y, omega):
    ''' Определяет правую часть ДУ примера 2
    omega - параметр'''
    return y*np.cos(omega*t)

# Параметр модели
omega = np.pi/2
# Параметры численного счета
t0 = 0
tf = 10
nt = 1000
# Массив точек (сетка) в которых будет находится решение
t_e = np.linspace(t0, tf, nt)
# Начальное условие
y0 = np.array([3])

f = partial(F_right2, omega=omega)
t_e = np.linspace(t0, tf, nt)
sol_2 = solve_ivp(f, [t0, tf], y0, t_eval=t_e, method='RK45',
                  rtol=1e-8, atol=1e-8)

def y_exact2(y0, t, omega):
    ''' Определяет точное решение ДУ,
        примера 2'''
    return y0*np.exp(np.sin(omega*t)/omega)

plt.figure(figsize=(8, 6))
plt.plot(sol_2.t, sol_2.y[0], label='Численное решение задачи (3) $y(t)$',
         linewidth=3.0)
plt.plot(t_e, y_exact2(y0, t_e, omega),
         label='Аналитическое решение $y_{exact}(t) $',
         linestyle='--', linewidth=3.0)
plt.xlabel('t', size=16)
plt.ylabel('$y(t)$', size=12)
plt.legend(loc='upper center', fontsize=11)
plt.show()