Задача 1: Линеаризованное уравнение на магнитный момент

Рассмотрим частный случай, когда уравнение на магнитный момент Ландау–Лифшица–Гильберта может быть сведено к решению уравнения на одну компоненту \(m_y\) (линейный осциллятор).

\[ \begin{eqnarray} \frac{d^2 m_y}{dt^2} + 2\alpha \omega_J \frac{d m_y}{dt} +\omega_F^2 m_y = \omega_F^2 G r \sin(\omega_J t) \label{eq4} \tag{4} \end{eqnarray} \]

с параметрами модели:

• G - отношение энергии Джозефсона к энергии магнитной анизотропии;

• r - константа спин-орбитального взаимодействия;

• \(\alpha\) - диссипация Гилберта;

• \(\omega_F\) - частота ферромагнитного резонанса.

Для проведения исследования динамики перейдем от одного дифференциального уравнения второго порядка к системе двух уравнений и разрешим их относительно производных, полагая \( m_y = y_1\):

\[\begin{split} \begin{eqnarray} \begin{cases} \frac{d y_1}{dt} = y_2, \\ \frac{d y_2}{dt} = - 2\alpha \omega_J y_2 -\omega_F^2 y_1 + \omega_F^2 G r \sin(\omega_J t). \end{cases} \label{eq5} \tag{5} \end{eqnarray} \end{split}\]

Начальные условия:

\[ \begin{eqnarray} y_1(0)=0.1, y_2(0)=0. \tag{6} \end{eqnarray} \]

import numpy as np
import matplotlib.pyplot as plt
from functools import partial
from scipy.integrate import solve_ivp
import seaborn as sns
sns.set()
sns.set(style="whitegrid")

Опредляем значения параметров модели и численного решения

# Параметры модели
G = 0.1
r = 0.1
omegaF = 0.5
alpha = 0.1
omegaJ = 1
# Параметры численного счета
t0 = 0
tf = 100
nt = 1000
# Массив точек (сетка) в которых будет находится решение
t_e = np.linspace(t0, tf, nt)
# Начальное условие
y0 = np.array([0.01, 0])

def my_t(t, S, G, r, alpha, omegaF, omegaJ):
    ''' Определяет правые части ДУ Задачи 1.
    G, r, alpha, omegaF,omegaJ - параметры модели
    S=[y1, y2] - вектор-фунция'''
    y1 = S[0]
    y2 = S[1]
    dy1 = y2
    dy2 = -2*alpha*omegaF*y2 - omegaF*omegaF*y1 + \
        omegaF*omegaF*G*r*np.sin(omegaJ*t)
    dS = [dy1, dy2]
    return dS

s = np.array([0.1, 0])
dS = my_t(0, s,  0.1, 0.1, 0.1, 0.5, 1)

dS

[0.0, -0.025]

f = partial(my_t, G=G, r=r, alpha=alpha,
            omegaF=omegaF, omegaJ=omegaJ)
t_e = np.linspace(t0, tf, nt)
s0 = np.array([0.0, 0])
sol_lin = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='RK45')

plt.figure(figsize=(8, 6))
plt.plot(sol_lin.t, sol_lin.y[0],
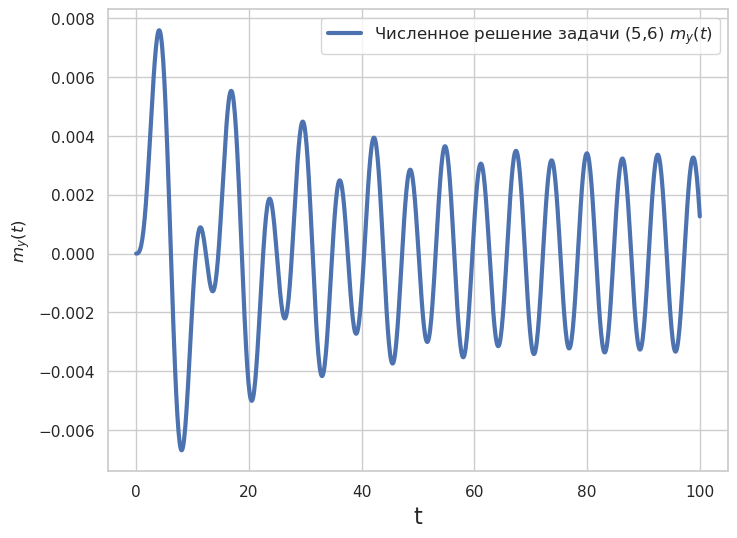
         label='Численное решение задачи (5,6) $m_y(t)$', linewidth=3.0)
plt.xlabel('t', size=16)
plt.ylabel('$m_y(t)$', size=12)
plt.legend(fontsize=12)
plt.show()