Задача 2. Периодичность появления интервалов переворота намагниченности в \(Ф0\) джозефсоновском переходе под воздействием импульса тока

Python-realization

Рассмотрим Python- реализацию программного кода, на основе которого получены результаты в статье:

[1] P. Kh. Atanasova, S.A. Panayotova, I.R. Rahmonov, Yu. M. Shukrinov, E.V. Zemlyanaya, and M. V. Bashashin. Periodicity in the Appearance of Intervals of the Reversal of the Magnetic Moment of a \(ϕ_0\) Josephson Junction. , JETP Letters, 2019, Vol. 110, No. 11, pp. 722–726

---

Схема перехода \(ϕ_0\):

• (S) сверхпроводящие слои

• (F) ферромагнитный слой

• (M) магнитный момент ферромагнитного слоя, ось которого направлена вдоль оси \(z\).

Математическая постановка задачи

Основные уравнение представлены в работе [1]. Ниже приведена задача Коши для системы уравнений в безразмерном виде. Динамика магнитного момента \(M\) рассматриваемой системы описывается уравнением Ландау–Лифшица–Гильберта:

\[\begin{split} \begin{eqnarray} && \frac{dm_x}{dt}=-\frac{1}{1+M^2\alpha^2} \left\{ m_y H_z -m_z H_y +\alpha [m_x (M,H) - H_x] \right\},\\ && \frac{dm_y}{dt}=-\frac{1}{1+M^2\alpha^2} \left\{ m_z H_x -m_x H_z +\alpha [m_y (M,H) - H_y] \right\},\\ && \frac{dm_z}{dt}=-\frac{1}{1+M^2\alpha^2} \left\{ m_x H_y -m_y H_x +\alpha [m_z (M,H) - H_z] \right\}, \label{eq7} \tag{7} \end{eqnarray} \end{split}\]

где \( M=[m_x, m_y, m_z] \) -компоненты магнитного момента.

Компоненты эффективного поля \(H=[H_x,H_y,H_z]\) зависит от джозефсоновской разности фаз \(\phi \) определются следующим образом:

\[\begin{split} \begin{eqnarray} && H_x (t)=0,\\ && H_y = G r \sin( \phi(t)-r m_y(t) ),\\ && H_z (t)= m_z(t), \end{eqnarray} \end{split}\]

при этом уравнение на джозефсоновскую разность фаз \(\phi (t)\) определяется из уранения на электрический ток \(I\) определяется через джозефсоновский контакт, измеренный в единицах критического тока \(I_c\):

\[ I= w \left( \frac{d\phi}{dt} - r \frac{dm_y}{dt}\right) +\sin(\phi- r m_y), \]

а именно:

\[ \begin{eqnarray} \frac{d\phi}{dt}= -\frac{1}{w}\left( \sin(\phi- r m_y) + r \frac{dm_y}{dt} \right)+\frac{1}{w} I, \label{eq8} \tag{8} \end{eqnarray} \]

с параметрами модели:

• G - отношение энергии Джозефсона к энергии магнитной анизотропии;

• r - константа спин-орбитального взаимодействия;

• \(\alpha\) - диссипация Гилберта;

• \(\omega_F\) - частота ферромагнитного резонанса;(не входит в уравнения!)

Начальные условия

Начальные условия предполагают, что все компонентны магнитного момента, кроме \(m_z\), равны нулю:

\[ \begin{eqnarray} m_x(0)=0, m_y(0)=0, m_z(0)=1, \phi(0) =0. \label{eq9} \tag{9} \end{eqnarray} \]

Вид тока

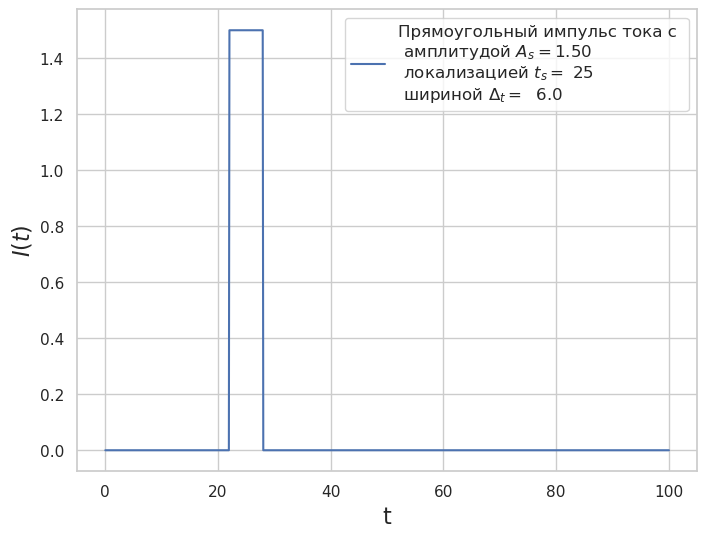
Ток \(I\) в уравнении (8) представляется в виде прямоугольного импульса:

\[\begin{split} \begin{eqnarray} I = I(t) = \begin{cases} A_s, & t \in \left[ t_s - \Delta t / 2, t_s + \Delta t / 2 \right], \\ 0, & otherwise. \end{cases} \end{eqnarray} \end{split}\]

• с амплитудой \(A_s\),

• локализацией \(t_s\),

• длительностью \(\Delta t\).

import numpy as np
import matplotlib.pyplot as plt
from functools import partial
from scipy.integrate import solve_ivp
import seaborn as sns
sns.set()
sns.set(style="whitegrid")

Определим функцию импулься тока и построим ее график

def I_pulse(t, As, t_s, delta_t):
    ''' Определяет пимпульс тока. Параметры
    As - амплитуда,
    t_s -локализация
    delta_t -длительность'''
    Ipuls = 0
    if t_s-1/2*delta_t <= t <= t_s+1/2*delta_t:
        Ipuls = As
    return Ipuls

Параметры импульса тока и численного решения

As = 1.5
t_s = 25
delta_t = 6
# Параметры численного счета
t0 = 0
tf = 100
nt = 1000
# Массивы точек, в которых находим значения тока
y_I = np.zeros([nt])
t_e = np.linspace(t0, tf, nt)
for i in range(nt):
    y_I[i] = I_pulse(t_e[i], As, t_s, delta_t)

plt.figure(figsize=(8, 6))
plt.plot(t_e, y_I, label='Прямоугольный импульс тока с ' +
         '\n амплитудой $A_s = $%4.2f' % As +
         '\n локализацией $t_s = $ %i' % t_s +
         '\n шириной $\Delta_t =$ %4.1f' % delta_t)
plt.xlabel('t', size=16)
plt.ylabel('$I(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

Определим правые части уравнений

def my_sfs(t, S,  G, r,  alpha, As, t_s, delta_t):
    ''' Определяет правые части ДУ Задачи 2.
    G, r, alpha, omegaF,omegaJ - параметры модели
    As, t_s, delta_t - параметры импульма тока
    S=[mx, my, mz, phi] - искомая вектор-фунция'''
    w = 1
    mx = S[0]
    my = S[1]
    mz = S[2]
    ph = S[3]
    Hx = 0
    Hy = G*r*np.sin(ph-r*my)
    Hz = mz
    H = [Hx, Hy, Hz]
    M = [mx, my, mz]
    m2 = np.dot(M, M)
    HdM = np.dot(H, M)
    alpha2 = -1/(1+alpha*alpha*m2)
    Iv = I_pulse(t, As, t_s, delta_t)
    dmx = alpha2 * ((my*Hz-mz*Hy) + alpha * (mx*HdM-Hx))
    dmy = alpha2 * ((mz*Hx-mx*Hz) + alpha * (my*HdM-Hy))
    dmz = alpha2 * ((mx*Hy-my*Hx) + alpha * (mz*HdM-Hz))
    dph = r * dmy - 1/w * np.sin(ph-r*my) + Iv/w
    dS = [dmx, dmy, dmz, dph]
    return dS

Проверяем на правильность

s = np.array([0, 0, 1, 0])
dS = my_sfs(0, s, 0.1, 0.1, 0.1, 1.5, 25, 5)
dS

[-0.0, -0.0, -0.0, 0.0]

Определим параметры модели

G = 18
r = 0.1
alpha = 0.1
As = 1.5
t_s = 25
delta_t = 6
t0 = 0
tf = 200

Находим численное решение с использованием библиотекой Scipy

# Параметры численного счета
t0 = 0
tf = 100
nt = 1000

f = partial(my_sfs, G=G, r=r, alpha=alpha,
            As=As, t_s=t_s, delta_t=delta_t)
t_e = np.linspace(t0, tf, nt)
s0 = np.array([0, 0, 1, 0])
sol_1 = solve_ivp(f, [t0, tf], s0, t_eval=t_e,
                  method='BDF', rtol=1e-8, atol=1e-8)

%matplotlib inline 
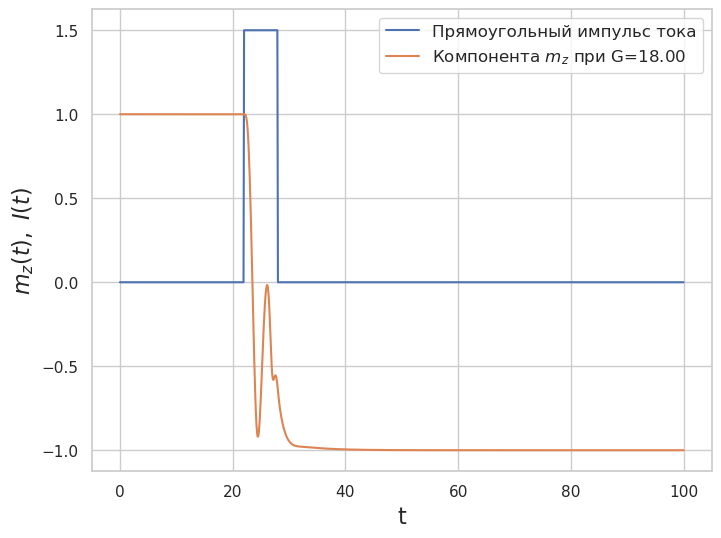
plt.figure(figsize = (8, 6))
plt.plot(t_e,y_I,  label= 'Прямоугольный импульс тока')
plt.plot(sol_1.t, sol_1.y[2], label= 'Компонента $m_z $ при G=%4.2f' %G)
plt.xlabel('t', size=16)
plt.ylabel('$m_z(t),~I(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

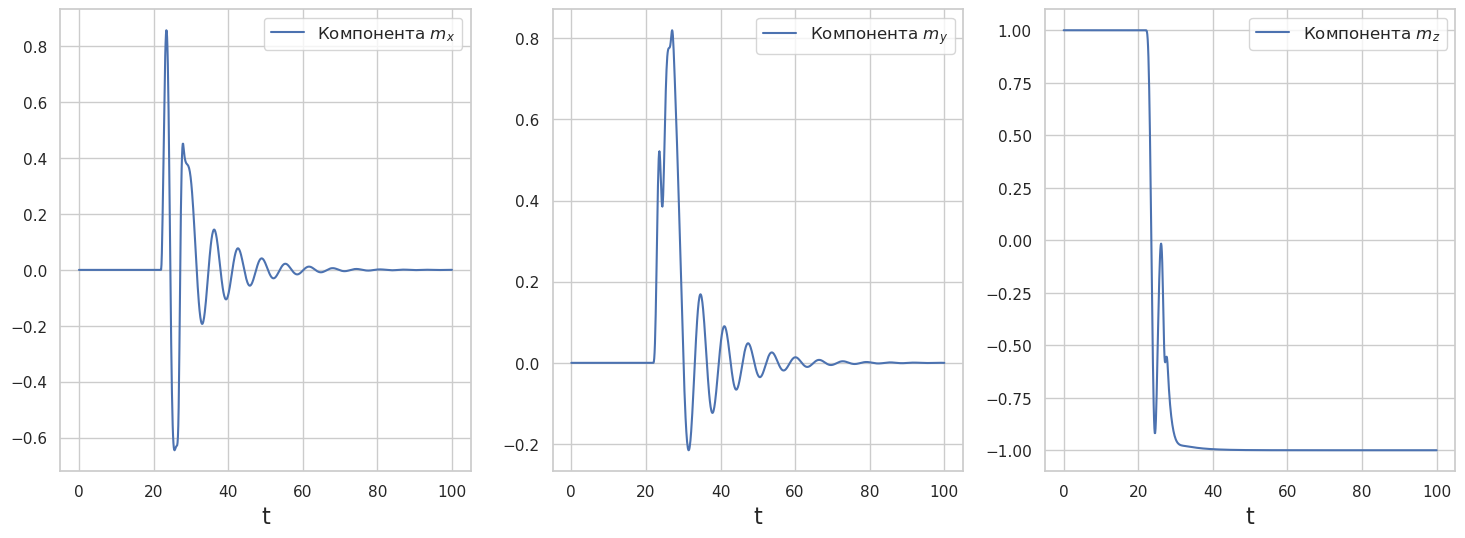
# Вывод графиков
plt.figure(figsize=(18, 6))
plt.subplot(1, 3, 1)
plt.plot(sol_1.t, sol_1.y[0], label='Компонента $m_x $')
plt.xlabel('t', size=16)
plt.legend(fontsize=12)
plt.subplot(1, 3, 2)
plt.plot(sol_1.t, sol_1.y[1], label='Компонента $m_y $')
plt.xlabel('t', size=16)
plt.legend(fontsize=12)
plt.subplot(1, 3, 3)
plt.plot(sol_1.t, sol_1.y[2], label='Компонента $m_z $')
plt.xlabel('t', size=16)
plt.legend(fontsize=12)
plt.show()

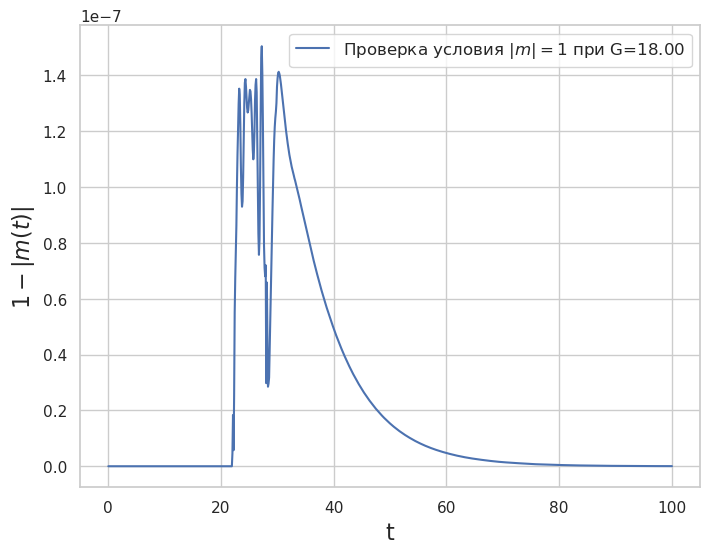
Проверка условия \(|m|=1\)

M_1 = 1 - np.sqrt(sol_1.y[0]**2 + sol_1.y[1]**2 + sol_1.y[2]**2)

plt.figure(figsize=(8, 6))
plt.plot(sol_1.t, M_1, label='Проверка условия $|m|=1 $ при G=%4.2f' % G)
plt.xlabel('t', size=16)
plt.ylabel('$1-|m(t)|$', size=16)
plt.legend(fontsize=12)
plt.show()

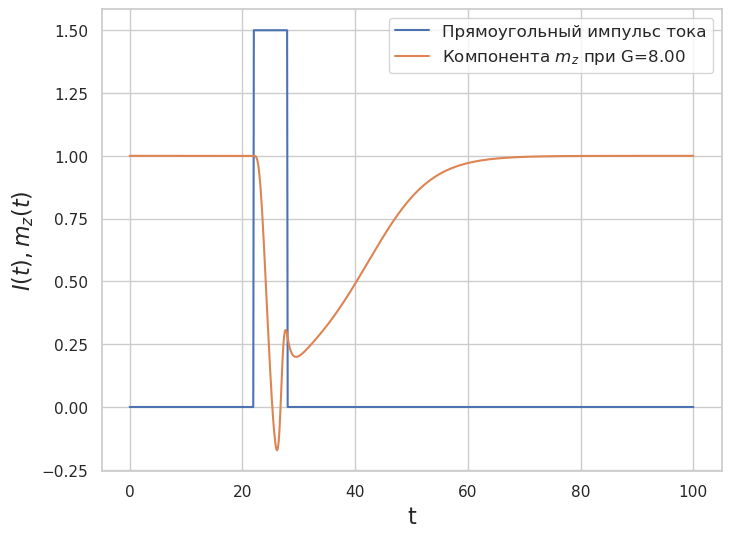
Расчеты при различных значениях параметров

Для анализа возможности обращения магнитного момента джозефсоновского перехода \(Ф0\) при различных зачениях параметров, проведем расчеты для G=8,9.

G = 8
f = partial(my_sfs, G=G, r=r, alpha=alpha,
            As=As, t_s=t_s, delta_t=delta_t)
t_e = np.linspace(t0, tf, nt)
s0 = np.array([0, 0, 1, 0])
sol_1 = solve_ivp(f, [t0, tf], s0, t_eval=t_e,
                  method='BDF', rtol=1e-8, atol=1e-8)

plt.figure(figsize=(8, 6))
plt.plot(t_e, y_I, label='Прямоугольный импульс тока')
plt.plot(sol_1.t, sol_1.y[2], label='Компонента $m_z $ при G=%4.2f' % G)
plt.xlabel('t', size=16)
plt.ylabel('$I(t), m_z(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

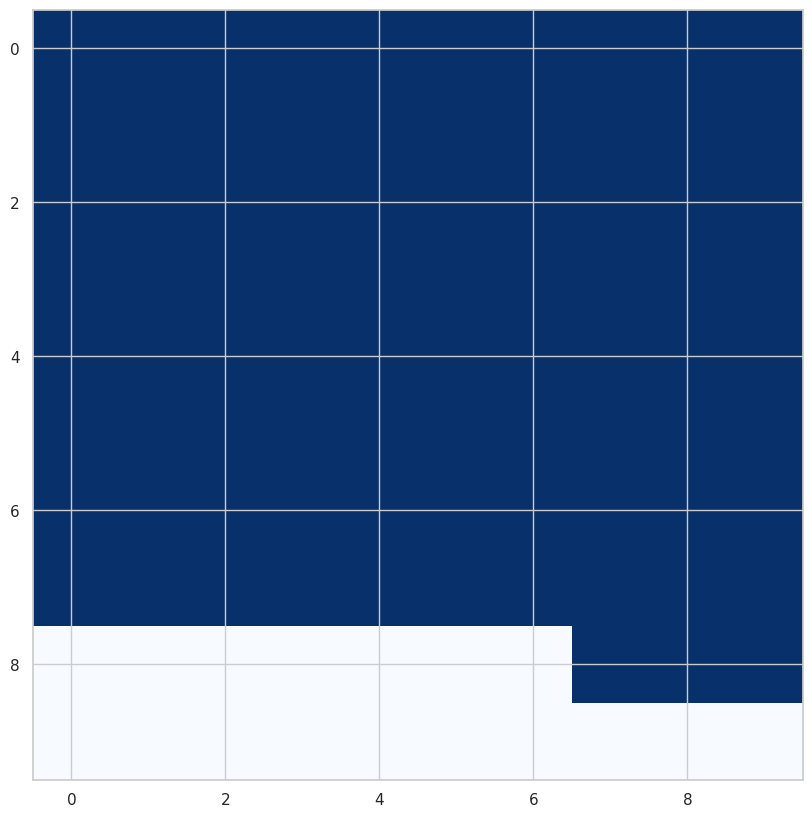
Проведение расчетов при различных знечениях параметров: плоскость \((\alpha, G)\)

# количество точек по каждому параметру при значении которых проводим расчеты
N = 10
G0 = 1
delta_G = 1
alpha0 = 0.1
delta_alpha = 0.01

alpG = np.zeros((N, N, 1)) + 1
alpG[1, 1, 0]

1.0

alpG.shape

(10, 10, 1)

# Параметры численного счета
t0 = 0
tf = 100
nt = 1000

%%time
for j in range(N):
    for i in range(N):

        G = G0 + delta_G*i
        alpha = alpha0+delta_alpha*j
        f = partial(my_sfs, G=G, r=r, alpha=alpha, \
                As=As, t_s=t_s, delta_t=delta_t)
        t_e = np.linspace(t0, tf, nt)
        s0 = np.array([0, 0, 1, 0])
        
        sol_i = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='BDF', rtol=1e-8, atol=1e-8) 
        if sol_i.y[2][nt-1] < 0:
            alpG[i, j, 0] =- 1

CPU times: user 20.1 s, sys: 62.3 ms, total: 20.2 s
Wall time: 20.2 s

Z1 = alpG.reshape(N, N)
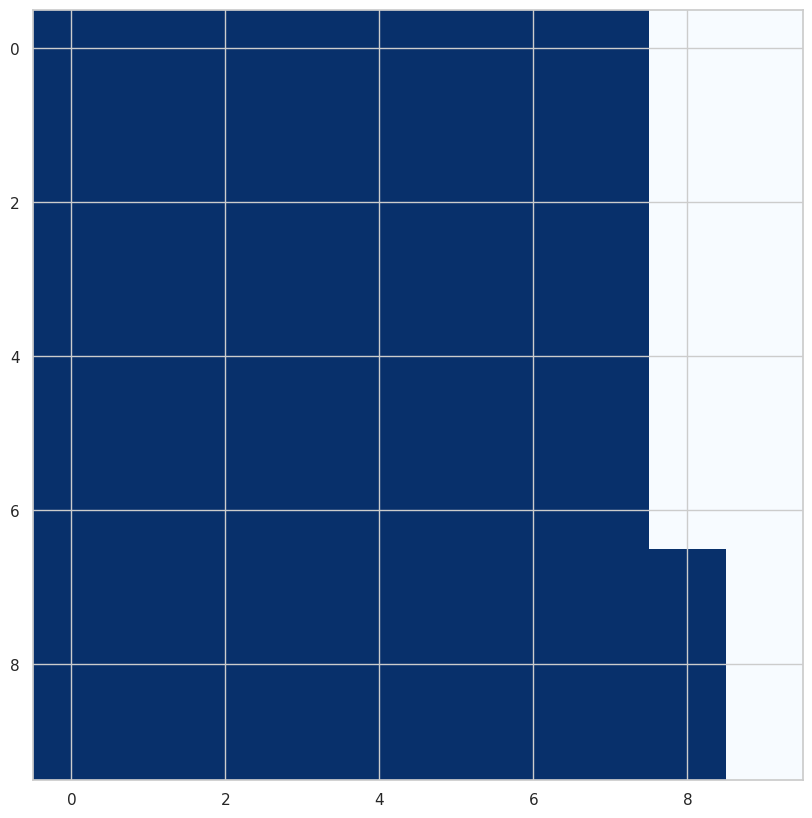
fig, ax = plt.subplots(figsize=(10, 10))
im = ax.imshow(Z1, cmap='Blues')

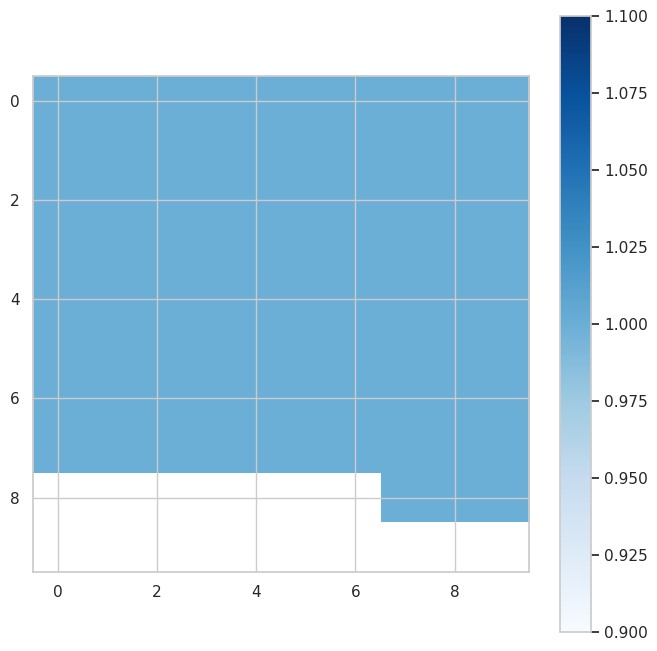
fig, ax1 = plt.subplots(figsize=(8, 8))
# mask out the negative and positve values, respectively
Zpos = np.ma.masked_less(alpG[:, :, 0], 0)
pos = ax1.imshow(Zpos, cmap='Blues', interpolation='none')
fig.colorbar(pos, ax=ax1)
plt.show()

Требуется параллелизация: можно провести расчеты для каждого набора параметров независимо

Параллельная реализация

import multiprocessing as mp
import time

print(f"Number of cpu: {mp.cpu_count()}")

Number of cpu: 80

n_cpu = mp.cpu_count()
n_cpu

80

Пример использования библиотеки Joblib

from joblib import Parallel, delayed
import numpy as np


def random_square(seed):
    np.random.seed(seed)
    random_num = np.random.randint(0, 10)
    return random_num**2

time_s = time.time()
results = Parallel(n_jobs=1)(delayed(random_square)(i) for i in range(10000))
time_f = time.time()
print(f'Execution time {time_f - time_s} s')

Execution time 0.3337514400482178 s

time_s = time.time()
results = Parallel(n_jobs=4)(delayed(random_square)(i) for i in range(10000))
time_f = time.time()
print(f'Execution time {time_f - time_s} s')

Execution time 1.3746991157531738 s

Нахождение решений задачи при различных значениях параметров в параллельном режиме

N = 10
G0 = 1
delta_G = 1
alpha0 = 0.1
delta_alpha = 0.01

alpG = np.zeros((N, N, 1)) + 1
alpG[1, 1, 0]

1.0

# Параметры численного счета
t0 = 0.0
tf = 100.0
nt = 1000

def funk_parall(k):
    i = k % N
    j = k // N
    mz_sol = 1
    G = G0 + delta_G*i
    alpha = alpha0 + delta_alpha*j

    f = partial(my_sfs, G=G, r=r, alpha=alpha,
                As=As, t_s=t_s, delta_t=delta_t)

    s0 = np.array([0, 0, 1, 0])
    t_e = np.linspace(t0, tf, nt)
    sol_i = solve_ivp(f, [t0, tf], s0, t_eval=t_e,
                      method='BDF', rtol=1e-8, atol=1e-8)

    if sol_i.y[2][nt-1] < 0:
        mz_sol = -1

    return mz_sol

time_s = time.time()
rez = Parallel(n_jobs=1)(delayed(funk_parall)(k) for k in range(N * N))
time_f = time.time()
print(f'Execution time {time_f - time_s} s')

Execution time 20.506993055343628 s

time_s = time.time()
rez = Parallel(n_jobs=4)(delayed(funk_parall)(k) for k in range(N*N))
time_f = time.time()
print(f'Execution time {time_f - time_s} s')

Execution time 5.93826961517334 s

alpGxy = np.zeros((N*N, 3)) + 1
alpGxy.shape

(100, 3)

for j in range(N):
    for i in range(N):
        G = G0+delta_G*i
        alpha = alpha0+delta_alpha*j
        alpGxy[i+j*N, 0] = G
        alpGxy[i+j*N, 1] = alpha

alpGxy[:, 2] = rez

X = alpGxy[:, 0]
Y = alpGxy[:, 1]
Z = alpGxy[:, 2]
Zc = (Z+1)/2

Z1 = Zc.reshape(N, N)

fig, ax = plt.subplots(figsize=(10, 10))
im = ax.imshow(Z1, cmap='Blues')