Задача 3. Ферромагнитный резонанс и динамика магнитного момента в системе “джозефсоновский переход-наномагнит”

В блокноте представлен инструментарий для исследования системы джозефсоновского перехода с наномагнитом на основе Python-реализации программного кода, на базе которого получены результаты в статье:

[1] Yu. M. Shukrinov, M. Nashaat, I. R. Rahmonov, and K. V. Kulikov. Ferromagnetic Resonance and the Dynamics of the Magnetic Moment in a “Josephson Junction–Nanomagnet” System. , JETP Letters, 2019, Vol. 110, No. 3, pp. 160–165

На основе данного программного кода возможно как всестороннее исследование динамики наномагнита, связанного с джозефсоновским переходом, так и моделирование существующих и возможных экспериментальных результатов. В частности, могут быть рассчитаны динамика намагниченности и сверхпроводящей фазы, средние значения проекций намагниченности, полного тока и сверхпроводящего тока при изменении различных параметров системы, а также максимальные значения амплитуды магнитной прецессии.

Схема системы

На Рис. 1 представлен схематический вид системы, состоящей из джозефсоновского перехода длины \(l\) и наномагнита, находящегося на расстоянии \(a\) от центра джозефсоновского контакта.

Рис. 1. Схематический вид рассматриваемой системы с эквивалентной схемой электрической цепи

Предполагается, что легкая ось наномагнита направлен вдоль оси \(y\), а напряжение \(V\) приложено к джозефсоновскому переходу.

Математическая постановка задачи

Динамика магнитного момента \(m\) рассматриваемой системы описывается уравнением Ландау-Лифшица-Гильберта [1], которое в нормированных единицах покомпонентно имеет вид :

\[\begin{split} \begin{eqnarray} && \frac{dm_x}{dt} = \frac{\Omega_F}{1 + m^2 \alpha^2} \left[h_y (m_z - \alpha m_x m_y) - h_z (\alpha m_x m_z + m_y) + \alpha h_x (m_y^2 + m_x^2) \right],\\ && \frac{dm_y}{dt} = \frac{\Omega_F}{1 + m^2 \alpha^2} \left[-h_x (\alpha m_x m_z + m_z) + h_z (m_x - \alpha m_y m_z) + \alpha h_y (m_x^2 + m_z^2) \right],\\ && \frac{dm_z}{dt} = \frac{\Omega_F}{1 + m^2 \alpha^2 + \Omega_F \alpha \epsilon k (m_x^2 + m_y^2) } \left[\alpha \epsilon [\sin(V t - k m_z) + V] (m_x^2 + m_y^2) - \right.\\ \label{eq1} \tag{1} \end{eqnarray} \end{split}\]

\[ \left. h_y (m_x + \alpha m_y m_z) + h_x (m_y - \alpha m_x m_z) \right], \]

где \(\epsilon = G k\) , \(m=[m_x, m_y, m_z]\) - нормированные компоненты магнитного момента, компоненты эффективного поля \(h = [h_x, h_y, h_z]\) определяются следующим образом:

\[\begin{split} \begin{eqnarray} && h_x (t)=0,\\ && h_y = m_y(t),\\ && h_z (t)= \epsilon [\sin(V t -k m_z(t)) +V] - \epsilon k \frac{dm_z}{dt}, \end{eqnarray} \end{split}\]

с параметрами модели:

• \(G\) - отношение энергии Джозефсона к энергии магнитной анизотропии;

• \(\alpha\) -параметр диссипации Гильберта;

• \(k\) - параметр связи;

• \(\Omega_F\) - частота ферромагнитного резонанса (ФМР).

Для численного исследования динамики магнитного момента наномагнита, связанного с джозефсоновским переходом, решается задача Коши для системы уравнений (1) с начальными условиями:

\( \begin{eqnarray} m_x(0)=0, m_y(0)=1, m_z(0)=0, \label{eq2} \tag{2} \end{eqnarray} \)

предполагающими, что все компонентны магнитного момента, кроме \(m_y\), равны нулю.

Инструментарий для численного моделирования

Для численного решения начальной задачи (1), (2) воспользуемся функцией solve_ivp библиотеки SciPy, примеры работы с которой представлены в разделе “Численное решение задачи Коши: библиотека SciPy” HLIT Jupyter Book. Для построения графиков будем использовать библиотеки Matplotlib и seaborn.

Ниже с комментариями представлены все шаги моделирования.

Подключаем необходимые библиотеки

import numpy as np
from scipy.integrate import odeint
from scipy.integrate import solve_ivp

from functools import partial

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
sns.set(style="whitegrid")

Определяем правые части уравнений

Для решения начальной задачи с использованием функции solve_ivp библиотеки SciPy, необходимо задать функцию, определяюшую правые части системы обыкновенных дифференциальных уравнений (1), описывающих динамику компонент магнитного момента \(M=[m_x, m_y, m_z]\) от времени \(t\).

def my_sfs(t, S, G, alpha, k, OmegaF, V):
    ''' Определяет правые части системы ОДУ (1),         
        G, alpha, k, OmegaF, V - параметры системы "джозефсоновский переход-наномагнит" '''
    w = 1

    mx = S[0]
    my = S[1]
    mz = S[2]

    epsilon = G * k
    M = [mx, my, mz]

    m2 = np.dot(M, M)
    alpha2 = OmegaF / (1 + alpha * alpha * m2)
    mxmy2 = mx * mx + my * my

    Hx = 0
    Hy = my

    alpha2mz = OmegaF / (1 + alpha * alpha * m2 + OmegaF * alpha *
                         epsilon * k * mxmy2)
    dmz_tmp = alpha2mz * (alpha * epsilon * (np.sin(V * t - k * mz) + V) *
                          mxmy2 - Hy * (mx + alpha * my * mz)
                          + Hx * (my - alpha * mx * mz))

    Hz = epsilon * (np.sin(V * t - k * mz) + V) - epsilon * k * dmz_tmp

    dmx = alpha2 * (Hy * (mz - alpha * mx * my) - Hz *
                    (alpha * mx * mz + my) + alpha * Hx * (my * my + mz * mz))
    dmy = alpha2 * (-Hx * (mz + alpha * mx * my) + Hz *
                    (-alpha * my * mz + mx) + alpha * Hy * (mx * mx + mz * mz))
    dmz = dmz_tmp

    dS = [dmx, dmy, dmz]
    return dS

Параметрами численного решения начальной задачи являются:

• t0 - начальное значение интервала интегрирования;

• tf - конечная точка интегрирования;

• nt - количество точек интервала интегрирования [t0, tf], в которых сохраняется решения системы ОДУ.

Массив точек задаем с помощью функции библиотеки Numpy

t_e = np.linspace(t0, tf, nt)

Функция solve_ivp поддерживает вызов различных методов решения задачи Коши: для нежестких систем, например, метод Рунге-Кутты ‘RK45’, и для жестких задач, например, неявный многошаговый метод переменного порядка ‘BDF’.

Для исследуемой системы проверием два этих метода решения для следующих значений физических параметров модели и параметров численного решения.

Отметим, что кроме исследования на жесткость системы, важным является и время расчета, которое можно измерить с помощью “магической команды” %%time (Cell Magic - магические команды ячейки, начинаются с %% и работают со всей ячейкой или несколькими строками ввода, подробнее см. статью).

# Физические параметры модели
G = 0.3
alpha = 0.001
k = 0.01
OmegaF = 0.5
V = 1.8

# Параметры численного счета
# Интервал интегрирования по времени [t0, tf]
t0 = 0
tf = 2000
nt = 50000

Отметим, что для вызова решатетеля solve_ivp для функции правых частей уравнений, содержащих параметры, вызов осуществляется с помощью функции partial, которая “замораживает” некоторую часть аргументов функции и/или ключевых слов.

Решение начальной задачи методом Рунге-Кутты (‘RK45’)

%%time
f = partial(my_sfs, G=G, alpha=alpha, k=k, OmegaF=OmegaF, V=V)
t_e = np.linspace(t0, tf, nt)

s0 = np.array([0, 1, 0]) # начальное условие 
sol_1_RK = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='RK45',
                  rtol=1e-8, atol=1e-9) 

CPU times: user 1.34 s, sys: 22.3 ms, total: 1.36 s
Wall time: 1.36 s

Полученное решение представлено в объекте sol_1_RK, содержащего массив точек sol_1_RK.t, посчитанное в них решение sol_1_RK.y и другие величины (более подробно см. документацию). На Рис. 2 преведена временная зависимость z-компоненты магнитного момента.

plt.figure(figsize=(10, 8))
plt.plot(sol_1_RK.t, sol_1_RK.y[2], label='Компонента $m_z$ при G = %4.2f' % G)
plt.xlabel('t', size=16)
plt.ylabel('$m_z(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

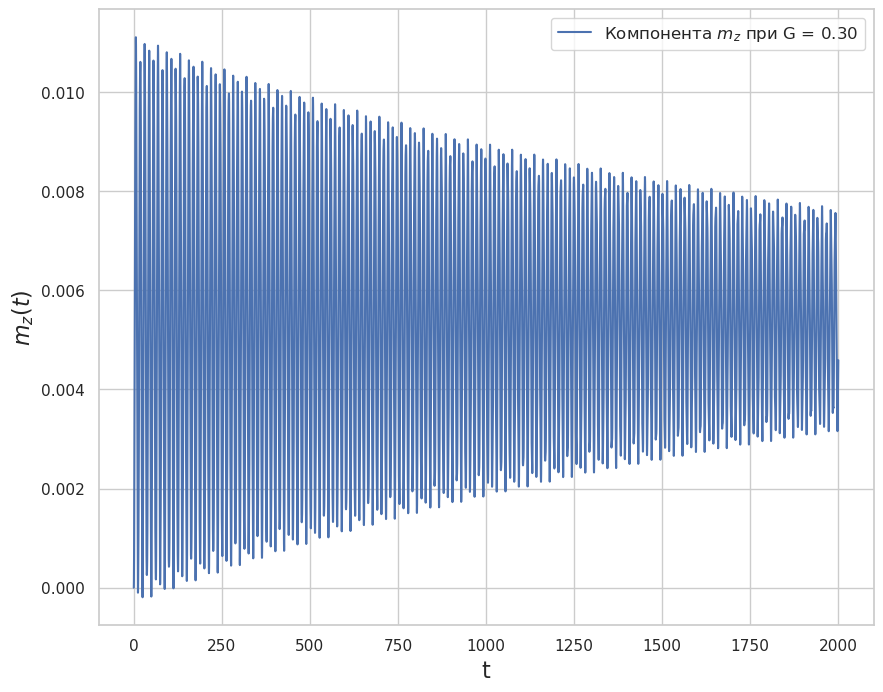
Рис. 2. Результаты расчета динамики проекции намагниченности на ось \(z\), полученные методом Рунге-Кутта

Решение начальной задачи многошаговым методом ‘BDF’

%%time
f = partial(my_sfs, G=G, alpha=alpha, k=k, OmegaF=OmegaF, V=V)
t_e = np.linspace(t0, tf, nt)

s0 = np.array([0, 1, 0])
sol_1_BDF = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='BDF', rtol=1e-8, atol=1e-9)

CPU times: user 5.56 s, sys: 20.8 ms, total: 5.58 s
Wall time: 5.59 s

plt.figure(figsize=(10, 8))
plt.plot(sol_1_BDF.t, sol_1_BDF.y[2], label='Компонента $m_z$ при G = %4.2f' % G)
plt.xlabel('t', size=16)
plt.ylabel('$m_z(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

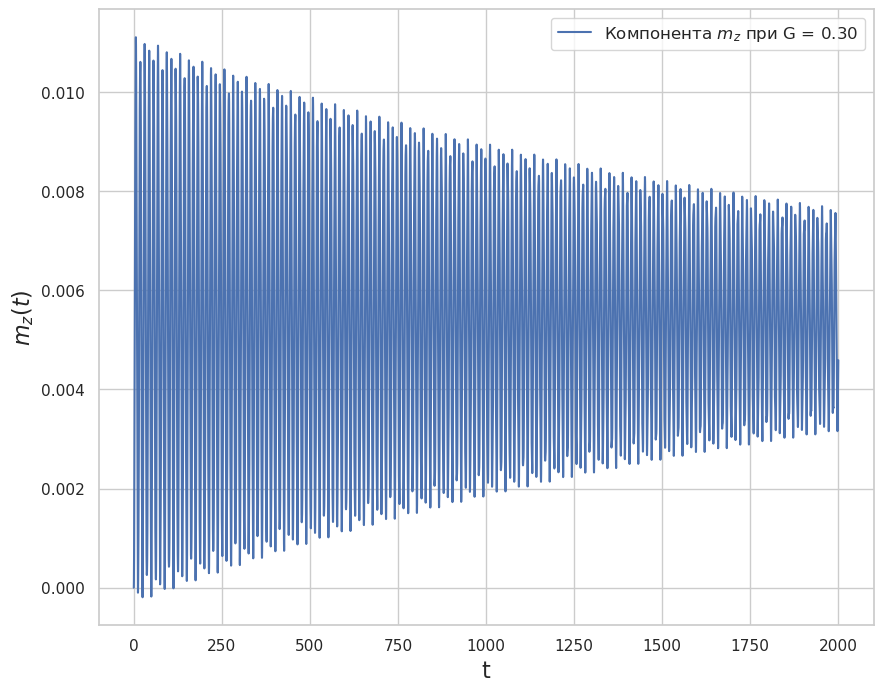
Рис. 3. Результаты расчета динамики проекции намагниченности на ось \(z\), полученные методом ВDF

Как видно из Рис. 2 и Рис. 3, полученные двумя методами результаты димамики магнитного момента совпадают.

Для получения количественной оценки найдем максимум по всем точкам нормы разности решений.

test = sol_1_BDF.y -sol_1_RK.y
test_err = (np.sqrt(test[0]**2+test[1]**2+ test[2]**2)).max()
print(test_err)

7.535913570757392e-08

Проведенное сравнение результатов показывает, что решения получены с заданной точностью, но время расчетов методом Рунге-Кутта в четыре раза меньше, поэтому, в дальнейших расчетах будем применять метод ‘RK45’.

Численное моделирование: исследование переориентации намагниченности в системе

Возможность переориентации намагниченности может быть показана при проведении расчетов при различных значениях параметров. Зафиксируем параметры \(k = 0.05\), \(\alpha = 0.1\), \(V=5\) и проведем расчеты для нескольких значений параметра \(G\).

# Зафиксированные физические параметры
alpha = 0.1
k = 0.05
OmegaF = 0.5
V = 5
# Параметры численного счеты
t0 = 0
tf = 120
nt = 600000

Расчет при \(G = 3\pi\)

G3 = 3*np.pi

f = partial(my_sfs, G=G3, alpha=alpha, k=k, OmegaF=OmegaF, V=V)
t_e = np.linspace(t0, tf,nt)

s0 = np.array([0, 1, 0])
sol_G3 = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='RK45',
                   rtol=1e-8, atol=1e-9)

plt.figure(figsize=(8, 6))
plt.plot(sol_G3.t, sol_G3.y[2], label='Компонента $m_z$ при G = %4.2f' % G3)
plt.xlabel('t', size=16)
plt.ylabel('$m_z(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

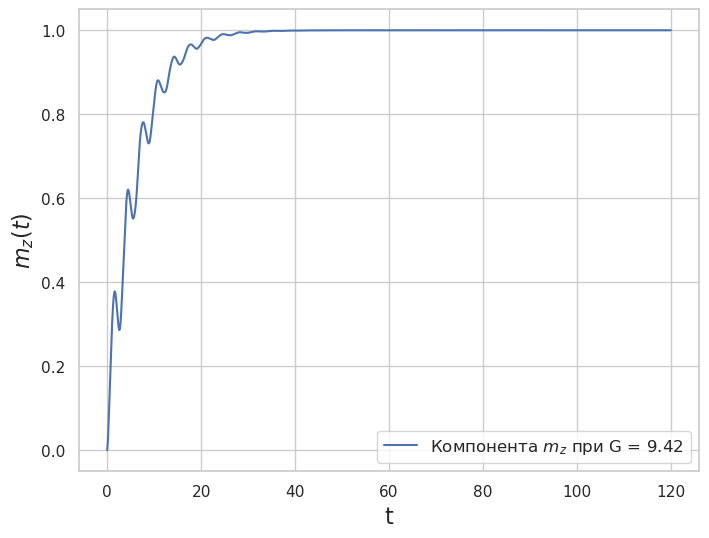
Рис. 4. Динамика компоненты \(m_z\) при значении параметра \(G=3\pi\) (\(k = 0.05\), \(\alpha = 0.1\), \(V=5\))

Расчет при \(G = \pi\)

G1 = np.pi

f = partial(my_sfs, G=G1, alpha=alpha, k=k, OmegaF=OmegaF, V=V)
t_e = np.linspace(t0, tf, nt)

s0 = np.array([0, 1, 0])
sol_G1 = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='RK45',
                   rtol=1e-8, atol=1e-9)

plt.figure(figsize=(8, 6))
plt.plot(sol_G1.t, sol_G1.y[2], label='Компонента $m_z$ при G = %4.2f' % G1)
plt.xlabel('t', size=16)
plt.ylabel('$m_z(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

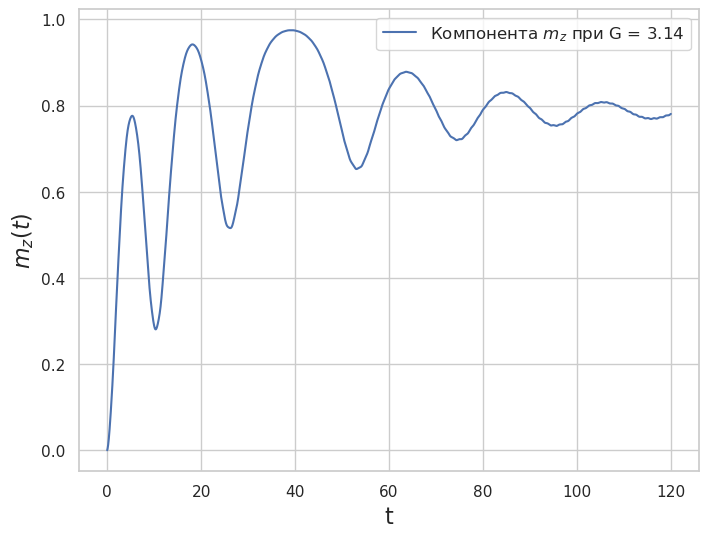
Рис. 5. Динамика компоненты \(m_z\) при значении параметроа \(G=\pi\) (\(k = 0.05\), \(\alpha = 0.1\), \(V=5\))

Расчет при \(G = 0.5\pi\)

G05 = 0.5*np.pi

f = partial(my_sfs, G=G05, alpha=alpha, k=k, OmegaF=OmegaF, V=V)
t_e = np.linspace(t0, tf, nt)

s0 = np.array([0, 1, 0])

sol_G05 = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='RK45',
                    rtol=1e-8, atol=1e-9)

plt.figure(figsize=(8, 6))
plt.plot(sol_G05.t, sol_G05.y[2], label='Компонента $m_z$ при G = %4.2f' % G05)
plt.xlabel('t', size=16)
plt.ylabel('$m_z(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

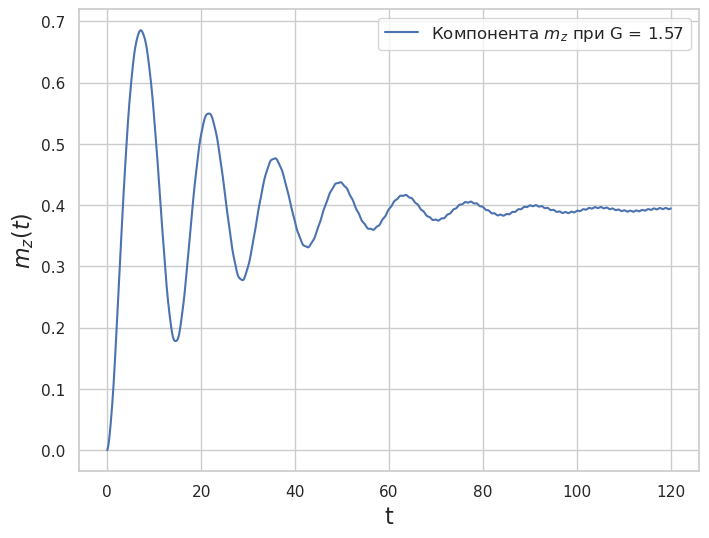
Рис. 6. Динамика компоненты \(m_z\) при значении параметра \(G=0.5\pi\) (\(k = 0.05\), \(\alpha = 0.1\), \(V=5\))

Расчет при \(G = 0.01\pi\)

G001 = 0.01*np.pi

f = partial(my_sfs, G=G001, alpha=alpha, k=k, OmegaF=OmegaF, V=V)
t_e = np.linspace(t0, tf, nt)

s0 = np.array([0, 1, 0])

sol_G001 = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='RK45',
                     rtol=1e-8, atol=1e-9)

plt.figure(figsize=(8, 6))
plt.plot(sol_G001.t, sol_G001.y[2],
         label='Компонента $m_z$ при G = %4.2f' % G001)
plt.xlabel('t', size=16)
plt.ylabel('$m_z(t)$', size=16)
plt.legend(fontsize=12)
plt.show()

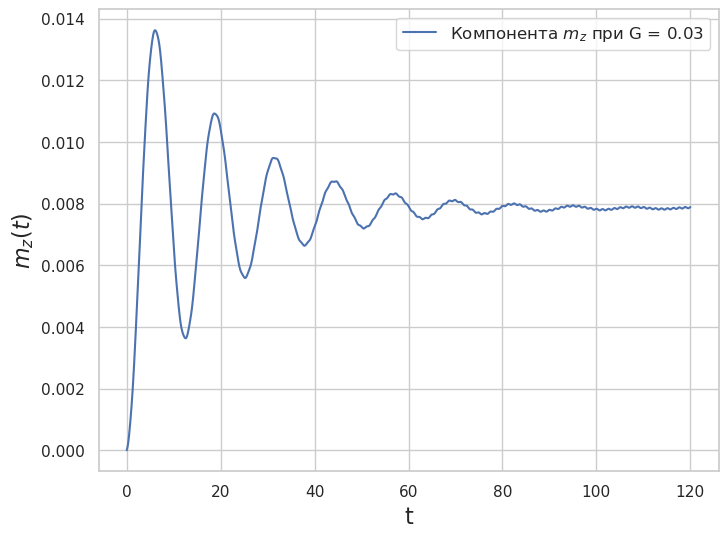
Рис. 7. Динамика компоненты \(m_z\) при значении параметра \(G=0.01\pi\) (\(k = 0.05\), \(\alpha = 0.1\), \(V=5\))

Для более наглядного представления построим результаты всех расчетов на одном рисунке:

plt.figure(figsize=(10, 8))

plt.plot(sol_G3.t, sol_G3.y[2], label='G = %4.2f' % G3, linewidth=2)
plt.plot(sol_G1.t, sol_G1.y[2], label='G = %4.2f' % G1, linewidth=2,
         color='black')
plt.plot(sol_G05.t, sol_G05.y[2], label='G = %4.2f' % G05, linewidth=2,
         color='green')
plt.plot(sol_G001.t, sol_G001.y[2], label='G = %4.2f' % G001, linewidth=2,
         color='red')

plt.xlabel('t', size=16)
plt.ylabel('$m_z(t)$', size=16)
plt.legend(loc=(0.772, 0.5), fontsize=12)
plt.savefig('gr-diffG-300dpi.jpg', bbox_inches='tight', dpi=300)

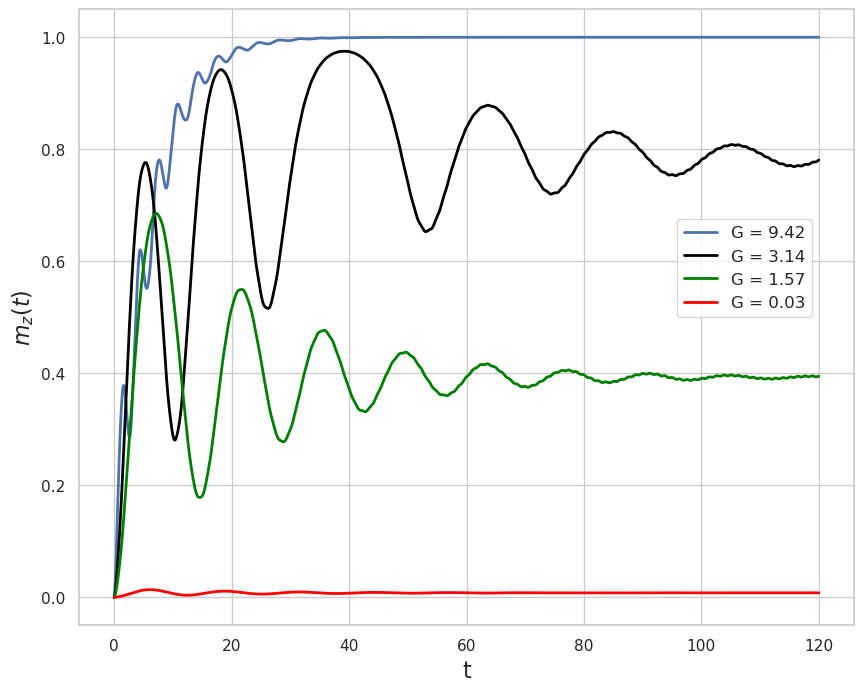
Рис. 8. Динамика компоненты \(m_z\) в зависимости от величины параметра \(G\) при \(k=0.05\), \(\alpha=0.1\) и \(V=5\)

Как видно из представленных результатов расчетов, компонента \(m_z\) в начальный момент \(m_z =0\) (магнитный момент направлен вдоль легкой оси - это ось \(y\)), при малых значениях параметра \(G\) временная зависимость \(m_z(t)\) выходит на определенное постоянное значение, а при \(G = 3\pi\), осциллируя, стремиться к единице, т.е. \(m_y\) обращается в ноль. Это и есть переориентация легкой оси магнетика.

Численное моделирование: проявление ФМР на зависимости \(m_z^{\max}(V)\)

Система “джозефсоновский переход - наномагнит” обладает богатой резонансной физикой. В этом разделе будет показано проявление ФМР на зависимости \(m_z^{\max}(V)\).

Отметим, что численное моделирование таких явлений требует проведения многочисленных расчетов при различных значениях параметров и является весьма времязатратным при проведении расчетов в последовательном режиме (с использованием одного ядра CPU). Технология распараллеливания по данным с использованием библиотеки joblib позволит существенно сократить время расчетов, что будет показано в следующем подразделе.

Инструментарий численного моделирования: параллелизация вычислений с использованием библиотеки joblib

Для исследования ФМР зафиксируем параметры \(G = 0.3\), \(k = 0.01\), \(\alpha= 0.001\) и \(\Omega_F = 0.5\), а для построения зависимости \(m_z^{\max}(V)\) зададим равномерную сетку по параметру \(V\):

\[V_j = V_{min}+ j \dot \Delta V, V_{min} = 0, \quad V_{max} = 1, \quad \Delta V = (V_{max} - V_{min})/N_{point}.\]

Для каждого значения \(V_j\) требуется решить задачи Коши, при этом, в зависимости от параметров системы, решение выходит на установившийся режим при различных значениях времени \(t\), что, при многочисленных расчетах, требует задания интервала интегрирования достаточно большим. Далее, для каждого полученного при значении параметра \(V=V_j\) решения \(m_z(t)\) находится максимальное значение на интервле установившегося режима и записывается в массив mz_max.

# Зафиксированные физические параметры
G = 0.3
k = 0.01
alpha = 0.3

OmegaF = 0.5

# Сетка по параметру V 
npoint = 200 
Vmin = 0
Vmax = 1
deltaV = (Vmax - Vmin) / npoint
Vgrid = np.zeros(npoint)

# Параметры численного счета (для решения начальной задачи при каждом значении V)
t0 = 0
tf = 32000
nt = 100000

Проведем расчеты в двух режимах: последовательном и параллельном.

Проведение расчетов в последовательном режиме

# массив для максимальных значений mz
mz_max = np.zeros(npoint)

Время расчета замерим с помощью “магической команды” %%time.

%%time

for j in range(Vgrid.shape[0]):
    V = Vmin + deltaV * j
    Vgrid[j] = V
    f = partial(my_sfs, G=G, alpha=alpha, k=k, OmegaF=OmegaF, V=V)
    t_e = np.linspace(t0, tf, nt)
    s0 = np.array([0, 1, 0])
    sol_j = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='RK45', rtol=1e-8, atol=1e-9)
    crop = sol_j.y[2][6249:]
    mz_max[j] =np.abs(crop).max()

CPU times: user 35min 8s, sys: 3.98 s, total: 35min 12s
Wall time: 35min 7s

plt.figure(figsize=(8, 6))
plt.plot(Vgrid[1:], mz_max[1:], label='Максимальное значение $m_z$ при'
         '\n $\u03b1$ = %5.3f, G = %5.3f, k = %5.3f' % (alpha, G, k))

plt.xlabel('V', size=16)
plt.ylabel('$m_z(t)^{\max}$', size=16)
plt.legend(fontsize=12)
plt.show()

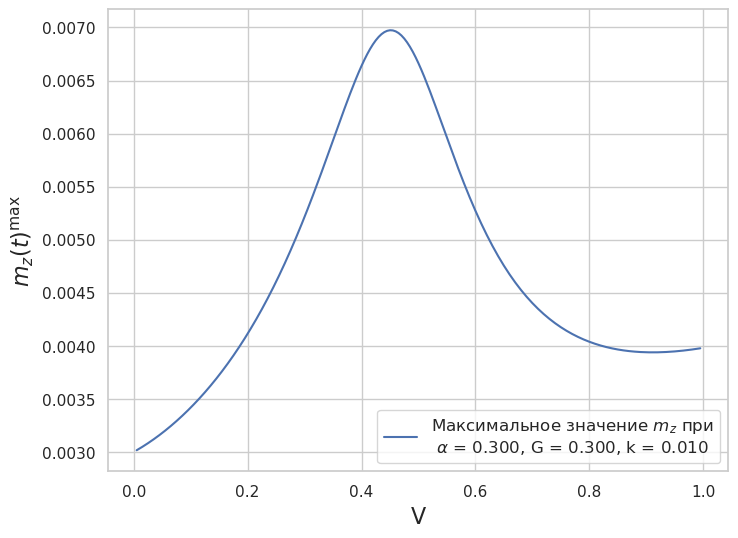
Рис. 9a. Расчет максимального значения амплитуды проекции намагниченности на ось \(z\)

Расчет занимает продолжительное время, поэтому проведем расчеты в параллельном режиме.

Проведение расчетов в параллельном режиме с использованием библиотеки joblib

Для распараллеливания вычислений по параметру \(V\) используем функционал библиотеки joblib, которая позволяет с помощью метода Parallel распределить вычисления по заданному количеству физических ядер процесоров n_jobs. Подробное описание возможностей библиотеки представленно в отдельном разле HLIT Jbook.

Подключение библиотеки joblib

import joblib
from joblib import Parallel, delayed
import time
import os

Проверка количества CPU-ядер/потоков

print(f"Number of cpu: {joblib.cpu_count()}")

Number of cpu: 80

mz_max = np.zeros(npoint)

Определим функцию для расчета в параллельном режиме

def funk_parall(jpar):
    V = Vmin + deltaV * jpar
    f = partial(my_sfs, G=G, alpha=alpha, k=k, OmegaF=OmegaF, V=V)
    t_e = np.linspace(t0, tf, 100000)
    s0 = np.array([0, 1, 0])
    sol_j = solve_ivp(f, [t0, tf], s0, t_eval=t_e,
                      method='RK45', rtol=1e-8, atol=1e-9)
    crop = sol_j.y[2][6249:]
    rezult = np.abs(crop).max()
    return rezult

Количество используемых потоков определяется параметров n_jobs. Для использования всех потоков необходимо использовать значение n_jobs=-1, для использования всех потоков, кроме одного, выбирается значение n_jobs=-2.

Для замеров времени выполнения воспользуемся функцией time() библиотеки модуля time.

t_start = time.time()
rez = Parallel(n_jobs=-1)(delayed(funk_parall)(jn) for jn in range(npoint))
t_finish = time.time()
print(f'Execution time {t_finish - t_start} s')

Execution time 95.63290619850159 s

rez1 = np.array(rez)

Vgrid = np.zeros(npoint)
for j in range(npoint):
    Vgrid[j] = Vmin + deltaV*j

Для того, чтобы убедится в правильности проведения расчетов в параллельном режиме построим еще раз полученную зависимость.

plt.figure(figsize=(8, 6))
plt.plot(Vgrid[1:], rez1[1:], label='Максимальное значение $m_z$ при'
         '\n $\u03b1$ = %5.3f, G = %5.3f, k = %5.3f' % (alpha, G, k))
plt.xlabel('V', size=16)
plt.ylabel('$m_z(t)^{\max}$', size=16)
plt.legend(fontsize=12)
plt.show()

Рис. 9b. Расчет максимального значения амплитуды проекции намагниченности на ось \(z\) при \(\alpha= 0.3\)

Сравнение времи расчетов в последовательном и параллельных режимах, показывает: при задействовании 80 потоков время вычислений сократилось в 27 раз.

Далее исследование резонансной физики будем проводить в параллельном режиме.

Численное моделирование: исследование ФМР

Сравнение функций максимальной амплитуды осцилляций при различных знчениях параметра диссипации \(\alpha\)

Покажем проявление ФМР на зависимости максимальной амплитуды осцилляций наномагнита \(m_z^{\max}\) от приложенного к джозефсоновскому переходу напряжения \(V\). На Рис. 9 показана зависимость \(m_z^{\max}(V)\) при \(\alpha= 0.3\). Проведем расчеты при малом значении этого параметра - \(\alpha= 0.001\).

Расчеты при \(\alpha = 0.001\)

alpha1 = 0.3
alpha=0.001
alpha2=alpha

npoint = 200
Vmin = 0
Vmax = 1

deltaV = (Vmax - Vmin) / npoint

G = 0.3
k = 0.01
OmegaF = 0.5
t0 = 0
tf = 32000

mz_max = np.zeros(npoint)

t_start = time.time()
rez2 = Parallel(n_jobs=30)(delayed(funk_parall)(jn) for jn in range(npoint))
t_finish = time.time()
print(f'Execution time {t_finish - t_start} s')

Execution time 120.5206663608551 s

plt.figure(figsize=(8, 6))
plt.plot(Vgrid[1:], rez2[1:], label='Максимальное значение $m_z$ '
         'при \n $\u03b1$=%5.3f, G = %5.3f, k = %5.3f' % (alpha1, G, k))

plt.xlabel('V', size=16)
plt.ylabel('$m_z(t)^{\max}$', size=16)
plt.legend(fontsize=12, bbox_to_anchor=(0.51,1))

<matplotlib.legend.Legend at 0x7f60c48b7c40>

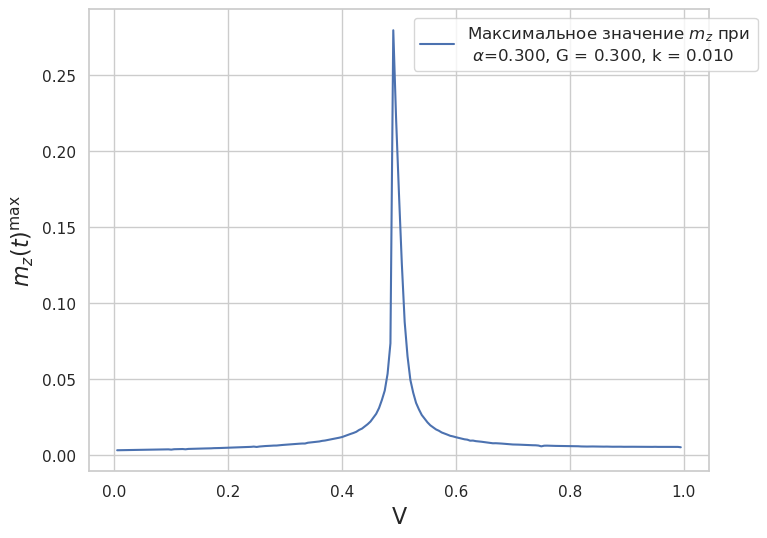
Рис. 10. Расчет максимального значения амплитуды проекции намагниченности на ось \(z\) при \(\alpha= 0.001\)

Покажем проявление ФМР на зависимости максимальной амплитуды осцилляций наномагнита \(m_z^{\max}\) от приложенного к джозефсоновскому переходу напряжения \(V\)

fig, ax1 = plt.subplots(figsize=(8, 6))
ax2 = ax1.twinx()

line1, = ax1.plot(Vgrid[1:], rez1[1:],
                  label=r'$ \alpha$ = %5.3f' % alpha1, color='r')
line2, = ax2.plot(Vgrid[1:], rez2[1:],
                  label=r'$ \alpha$ = %5.3f' % alpha2)

ax1.set_ylabel(r'$m_z^{\max}, \alpha$ = %5.3f' % alpha1)
ax2.set_ylabel(r'$m_z^{\max}, \alpha$ = %5.3f' % alpha2)

ax1.set_xlabel('V', size=16)

plt.grid(False)

ax2.legend(handles=[line1, line2])

plt.text(0,0.25, 'G = %5.3f, k = %5.3f' % (G, k), backgroundcolor='0.8')

Text(0, 0.25, 'G = 0.300, k = 0.010')

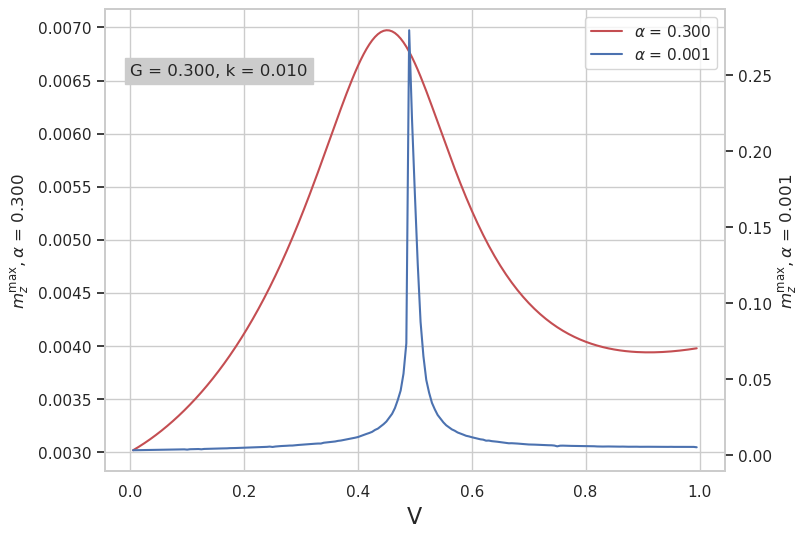
Рис. 11. Зависимости \(m_z^{\max}(V)\) при различных значениях параметра диссипации

Из Рис. 11 видно заметное уширение резонансного пика вызванное увеличение диссипации \(\alpha\). Отметим также, что с увеличением диссипации усиливается проявление нелинейности уравнений, максимум пика смещается влево и он становится заметно ассиметричным.

Расчеты при различных значениях параметра \(G\) и фиксированных значениях остальных параметров.

Покажем влияние отношения джозефсоновской энергии к энергии наномагнита \(G\) на ширину ФМР для \(m_z^{\max}\)

Расчеты при \(G = 0.1\)

G = 0.1
G1 = G

npoint = 200
Vmin = 0
Vmax = 1

deltaV = (Vmax-Vmin) / npoint

alpha = 0.1
k = 0.01
OmegaF = 0.5
t0 = 0
tf = 32000

mz_max = np.zeros(npoint)

t_start = time.time()
rez_G1 = Parallel(n_jobs=30)(delayed(funk_parall)(jn) for jn in range(npoint))
t_finish = time.time()
print(f'Execution time {t_finish - t_start} s')

Execution time 88.503751039505 s

Расчеты при \(G = 3\pi\)

G = 3*np.pi
G2 = G

npoint = 200
Vmin = 0
Vmax = 1

deltaV = (Vmax-Vmin) / npoint

alpha = 0.1
k = 0.01
OmegaF = 0.5
t0 = 0
tf = 32000

mz_max = np.zeros(npoint)  # massiv max value mz

t_start = time.time()
rez_G2 = Parallel(n_jobs=30)(delayed(funk_parall)(jn) for jn in range(npoint))
t_finish = time.time()
print(f'Execution time {t_finish - t_start} s')

Execution time 179.17283153533936 s

fig, ax1 = plt.subplots(figsize=(8, 6))
ax2 = ax1.twinx()

line1, = ax1.plot(Vgrid[1:], rez_G1[1:], label='G = %5.3f' % G1, color='r')
line2, = ax2.plot(Vgrid[1:], rez_G2[1:], label='G = %5.3f' % G2)

ax1.set_ylabel(r'$m_z^{\max}$, G = %5.3f' % G1)
ax2.set_ylabel(r'$m_z^{\max}$, G = %5.3f' % G2)

ax1.set_xlabel('V', size=16)

plt.grid(False)

ax2.legend(handles=[line1, line2])

plt.text(0.0, 0.55, r'$\alpha$ = %5.3f, k = %5.3f' % (alpha, k),
         backgroundcolor='0.8')

Text(0.0, 0.55, '$\\alpha$ = 0.100, k = 0.010')

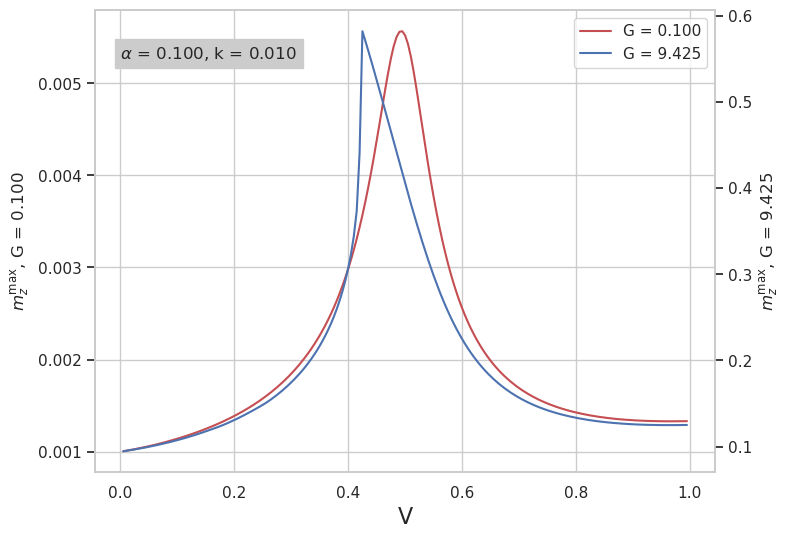
Рис. 12. Зависимости \(m_z^{\max}(V)\) при различных значениях параметра \(G\)

На Рис. 12 виден заметный сдвиг максимума резонансного пика влево, вызванный изменение отношения джозефсоновской энергии к магнитной.