Практическое занятие в рамках Осенней ИТ-школы ОИЯИ-2024

Математическое моделирование джозефсоновского перехода сверхпроводник/ферромагнетик/сверхпроводник на поверхности трехмерного топологического изолятора

Зуев М.И., Нечаевский А.В., Рахмонов И.Р., Рахмонова А.Р., Стрельцова О.И.

Работа поддержана грантом РНФ № 22-71-10022.

Проект «Математическое моделирование сверхпроводящих наноструктур с магнетиком для исследования возможностей контроля намагниченности и магнитных возбуждений с использованием высокопроизводительных вычислительных систем»

1. Введение: Исследование поведения подынтегральной функции при различных значениях параметров, численное интегрирование и аппроксимация интегралов при различных значениях параметров

Особенности вычисления интеграла:

\[j_s = \int\limits_{-\pi/2}^{\pi/2} \cos\varphi \exp{\left(-\frac{d}{\cos(\varphi)}\right)} \cos (r m_x \tan\varphi) d\varphi.\]

Подынтерральная функция на концах интрервала интегрирования не определена, однако

\[\lim_{\varphi \to \pm\frac{\pi}{2}} f( m_x, r, d, \varphi ) = 0.\]

Параметры модели:

• \(d\) - безразмерная длина контакта, \(d \in [0.1,0.8]\);

• \(r\) - безразмерный параметр, определяющий величину спин-орбитального взаимодействия, \(r \in [0.1,2]\);

• \(G\) - отношение энергии Джозефсона к энергии магнитной анизотропии, \(G \in [0.1,10]\);

• \(\alpha\) - диссипация Гилберта \(\alpha \in [0.01,0.2]\);

• \(wF = 1\).

Функция, подлежащая определению, значения которой при вычиcлении интеграла играет роль параметра: \(m_x\) - компонета намагниченности.

Подключение необходимых библиотек

import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

%matplotlib inline

# use seaborn plotting defaults
sns.set()
sns.set(style="whitegrid")

params = {'axes.labelsize': 12,
          'axes.titlesize': 16,
          'legend.fontsize':12
         }
plt.rcParams.update(params)

Определим подынтегральную функцию

def funct_js(phi, mx, r, d):
    ''' Defines the integrand in the definition of current js,
        mx, r, d - parameters '''
    return (np.cos(phi) * np.exp(-d / np.cos(phi)) * np.cos(r*mx*np.tan(phi)))

d = 0.8
r = 1.1
mx = 0.5

funct_js(-np.pi/2, mx, r, d)

0.0

phi = np.linspace(-np.pi/2, np.pi/2, 300, endpoint=True)

y = funct_js(phi, mx, r, d)
print(y.max(), y.argmax())

0.4493159274797835 149

plt.figure(figsize=(8, 6), dpi=150)
plt.scatter(phi, y, edgecolor="red", s=10,
            label=r'$r=%6.2f, d=%6.2f, m_x=%6.2f$' % (r, d, mx))
plt.plot(phi, y)
plt.xlabel(r"$\varphi$")
plt.ylabel("$F_{js}$")

plt.title(r"Зависимость подынтегральной функции $F_{js}$ от угла $\varphi$")
plt.legend(loc='upper right', fontsize=12)

plt.show()

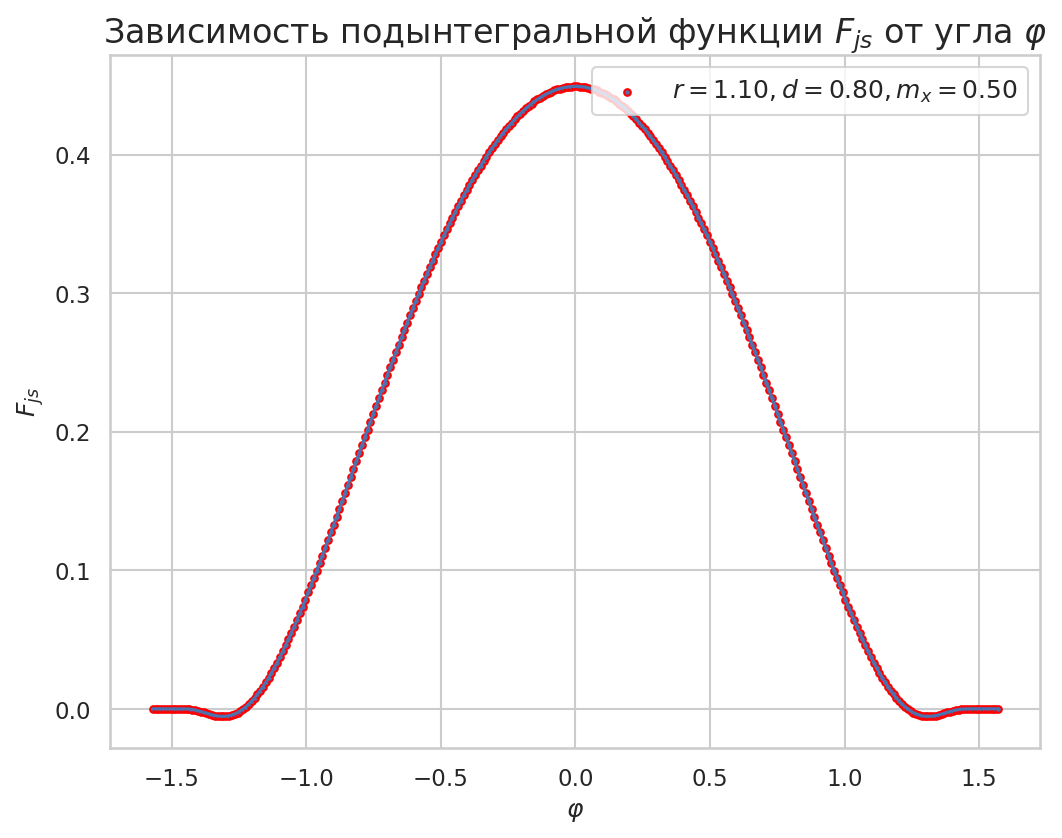
Численное интегрирование с использованием библиотеки SciPy

Воспользуемся функцией quad:

quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50, complex_func=False)[source]

Compute a definite integral. Integrate func from a to b (possibly infinite interval) using a technique from the Fortran library QUADPACK.

from scipy.integrate import quad

%%time
js = quad(funct_js, -np.pi/2, np.pi/2, args=(mx,r,d))
js

CPU times: user 1.95 ms, sys: 0 ns, total: 1.95 ms
Wall time: 1.96 ms

(0.6373655635798351, 7.628367821953997e-11)

Время интегрирования (все параметры зафиксированы, кроме \(m_x\))

Npoint = 1000
arr_mx = np.linspace(-1, 1, Npoint, endpoint=True)
# The integral of the function in the specified interval of phi
arr_js = np.zeros(Npoint, dtype=np.float64)
# An estimate of the absolute error in the result
arr_err = np.zeros(Npoint, dtype=np.float64)

arr_js .shape, arr_mx.shape

((1000,), (1000,))

%%time
for ind in range(Npoint):
    mx = arr_mx[ind]
    arr_js[ind], arr_err[ind] = quad(funct_js, -np.pi/2, np.pi/2, args=(mx,r,d))

CPU times: user 1.46 s, sys: 0 ns, total: 1.46 s
Wall time: 1.46 s

plt.figure(figsize=(8, 6), dpi=150)
plt.scatter(arr_mx, arr_js, edgecolor="red", s=10,
            label=r'$r=%6.3f, d=%6.3f$' % (r, d))
plt.xlabel("$m_x$")
plt.ylabel("$j_{s}$")

plt.title("Зависимость $j_s$ от $m_x$")
plt.legend()

plt.show()

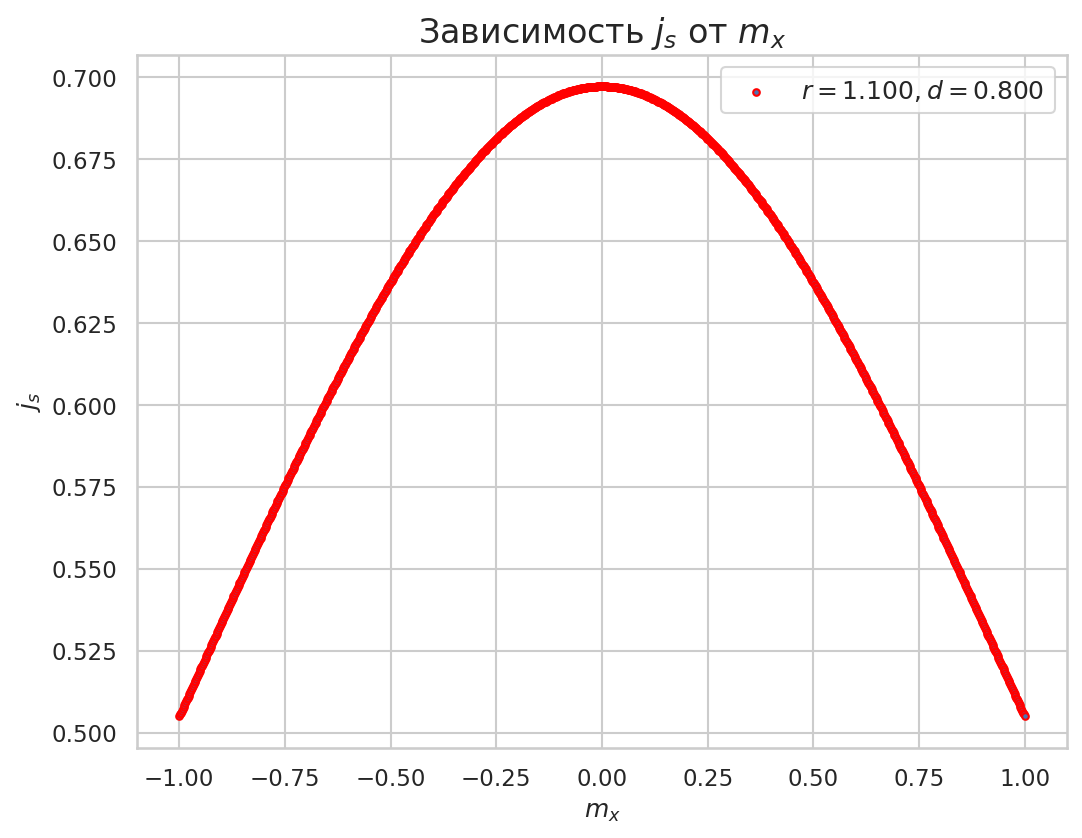
Как в интерактивном режиме посмотреть вид функции при изменении параметров?

Интерактивное управление в Jupyter Notebooks: библиотека IPywidgets

Для решения задач инерактивного управления параметрами воспользуемся библиотекой IPywidgets (См. ссылку). С помощью этой библиотеки блокнот Jupyter превращается в диалоговую панель, удобную для визуализации и работы с данными.

Для работа с IPywidgets создаем ячейку с:

import ipywidgets as widgets
from ipywidgets import interact, interact_manual, Label

Список доступных виджетов (Widget List) можно найти на сайте библиотеки.

Однако, в библиотеке есть удобная функция (ipywidgets.interact), котороя автоматически создает элементы управления пользовательского интерфейса (UI) для интерактивного изучения кода и данных. Это самый простой способ начать использовать виджеты IPython.

Мы воспользуемся конструкцией (декоратор):

@interact

которая автоматически создаёт и текстовое поле и слайдер для выбора колонки и числа. Декоратор смотрит на введённые параметры и создаёт панель диалогового управления, основываясь на типах данных.

Пример

import ipywidgets as widgets
from ipywidgets import interact, interact_manual, Label

%matplotlib widget 

@interact(mx=1.0, r=0.1, d=0.8, phi=np.pi/8)
def funct_js(phi, mx, r, d):
    ''' Defines the integrand in the definition of current js,
        mx, r, d - parameters '''
    return (np.cos(phi) * np.exp(-d / np.cos(phi)) * np.cos(r*mx*np.tan(phi)))

@interact
def show_js_mx(mx=(-1.0, 1.0, 0.1), r=(0.1, 2.0, 0.1), d=(0.1, 0.8, 0.1)):
    phi = np.linspace(-np.pi/2, np.pi/2, 300, endpoint=True)
    fig = plt.figure(figsize=(8, 6))
    plt.scatter(phi, funct_js(phi, mx, r, d), edgecolor="red", s=10,
                label=r'$r=%6.3f, d=%6.3f$' % (r, d))
    plt.plot(phi, funct_js(phi, mx, r, d))
    plt.xlabel(r"$\varphi$", fontsize=14)
    plt.ylabel("$j_{s}$", fontsize=14)
    plt.title(r"Зависимость $f$ от угла $\varphi$", fontsize=16)
    plt.legend(loc='upper right', fontsize=13)
    plt.show()

Для дальнейших исследований представляет интерес рассмотрение поведения функции тока \(j_s\) и интегралов \(I_x\) и \(I_y\) при различных значениях параметров.

Поведение функции тока \(j_s\) при различных значениях параметров

@interact
def show_funct_js(r=(0.1, 2.0, 0.1), d=(0.1, 0.8, 0.1)):
    Npoint = 1000  # количество точек (число вызовов функции интегрирования)
    arr_mx = np.linspace(-1, 1, Npoint, endpoint=True)
    arr_js = np.zeros(Npoint, dtype=np.float64)
    arr_err = np.zeros(Npoint, dtype=np.float64)
    for ind in range(Npoint):
        mx = arr_mx[ind]
        # интегрируем для каждого
        arr_js[ind], arr_err[ind] = quad(funct_js, -np.pi/2, np.pi/2,
                                         args=(mx, r, d))

    fig = plt.figure(figsize=(8, 6))
    plt.scatter(arr_mx, arr_js, edgecolor="red", s=10,
                label=r'$r=%6.3f, d=%6.3f$' % (r, d))
    plt.xlabel("$m_x$ ", fontsize=14)
    plt.ylabel("$j_{s}$", fontsize=14)

    plt.title("Зависимость $j_s$  от параметра  $m_x$ ", fontsize=16)
    plt.legend(fontsize=13)

    plt.show()

Вывод: функция имеет вид квадратичной (или многочлена четной степени)

Поведение интегралов \(I_x\) и \(I_y\) при различных значениях параметров

def funct_Ix(phi, mx, r, d):
    ''' Defines the integrand in the definition of current Ix,
        mx, r, d - parameters'''
    return (np.sin(phi) * np.exp(-d / np.cos(phi)) * np.sin(r*mx*np.tan(phi)))

def funct_Iy(phi, mx, r, d):
    ''' Defines the integrand in the definition of current Iy,
        mx, r, d - parameters'''
    return (np.cos(phi) * np.exp(-d / np.cos(phi)) * np.cos(r*mx*np.tan(phi)))

@interact
def show_funct_js(r=(0.1, 2.0, 0.1), d=(0.1, 0.8, 0.1)):
    Npoint = 1000  # количество точек (число вызовов функции интегрирования)
    arr_mx = np.linspace(-1, 1, Npoint, endpoint=True)
    arr_js = np.zeros(Npoint, dtype=np.float64)
    arr_err = np.zeros(Npoint, dtype=np.float64)
    for ind in range(Npoint):
        mx = arr_mx[ind]
        # интегрируем для каждого
        arr_js[ind], arr_err[ind] = quad(funct_Ix, -np.pi/2, np.pi/2,
                                         args=(mx, r, d))

    fig = plt.figure(figsize=(8, 5))
    plt.scatter(arr_mx, arr_js, edgecolor="red", s=10,
                label=r'$r=%6.3f, d=%6.3f$' % (r, d))
    plt.xlabel("$m_x$", fontsize=14)
    plt.ylabel("$I_{x}$", fontsize=14)

    plt.title("Зависимость $I_х$ от параметра $m_x$", fontsize=16)
    plt.legend(fontsize=13)

    plt.show()

Вывод: функция имеет вид кубической параболы (или многочлена нечетной степени)

Подходы к ускорению вычислений.

Аппросимация вычисленных интегралов для \(m_x \in [-1,1]\)

Для аппроксимации интеграла воспользуемся модулем \(scipy.optimize\) библиотеки Scipy, функцией curve_fit:

curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=None, bounds=(-inf, inf), method=None, jac=None, *, full_output=False, nan_policy=None, **kwargs)[source]

❓ Какую функцию выбрать?

Рассмотрим многочлены: $\(P_n(x), n = 2, 4,\dots.\)$

from scipy.optimize import curve_fit

# область изменения параметра mx
xnew = np.linspace(-1, 1, 2000, endpoint=True)

def func_P2(x, a, b, c):
    '''Defines a polynomial of the second degree'''
    return a*x*x + b*x + c

print(func_P2.__doc__)

Defines a polynomial of the second degree

# значения параметров
d = 0.8
r = 1.1
# массивы
Npoint = 1000
arr_mx = np.linspace(-1, 1, Npoint, endpoint=True)
arr_js = np.zeros(Npoint, dtype=np.float64)
arr_err = np.zeros(Npoint, dtype=np.float64)
# вычисление интегралов
for ind in range(Npoint):
    mx = arr_mx[ind]
    arr_js[ind], arr_err[ind] = quad(funct_js, -np.pi/2, np.pi/2,
                                     args=(mx, r, d))

# popt: optimal values for the parameters a, b, c
popt, pcov = curve_fit(func_P2, arr_mx, arr_js)
popt, pcov

(array([-1.98716968e-01,  2.15121365e-10,  6.91486558e-01]),
 array([[ 2.36340219e-07, -8.92887991e-10, -7.89996399e-08],
        [-8.92887991e-10,  9.50670530e-10,  3.64076821e-10],
        [-7.89996399e-08,  3.64076821e-10,  4.74284659e-08]]))

pcov.max()

2.363402187817121e-07

# Deviation error on parameters a, b, c
perr = np.sqrt(np.diag(pcov))
perr

array([4.86148351e-04, 3.08329455e-05, 2.17780775e-04])

plt.figure(figsize=(8, 5))
plt.scatter(arr_mx, arr_js, edgecolor="red", s=5,
            label=r'$r=%6.3f, d=%6.3f$' % (r, d))
plt.plot(arr_mx, func_P2(arr_mx, *popt), 'b-',
         label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
plt.xlabel("$m_x$")
plt.ylabel("$j_{s}$")

plt.title("Зависимость $j_s$ от параметра $m_x$")
plt.legend()

plt.show()

Аппроксимация многочленом степени \(n> 2\)

Для решения задачи аппроксимации возможно применить различные подходы, например, реализованный в библиотеке Numpy polyfit или подход в библиотеке Scipy: scipy.odr.polynomial, который и применим далее:

from scipy import odr
poly_model = odr.polynomial(order) 

Factory function for a general polynomial model.

Подробнее о методе ODR (Orthogonal distance regression) Можно прочитать в документации.

Многочлен второй степени \(P_2\)

# значения параметров
d = 0.8
r = 1.1
# массивы
Npoint = 1000
arr_mx = np.linspace(-1, 1, Npoint, endpoint=True)
arr_js = np.zeros(Npoint, dtype=np.float64)
arr_err = np.zeros(Npoint, dtype=np.float64)
# вычисление интегралов
for ind in range(Npoint):
    mx = arr_mx[ind]
    arr_js[ind], arr_err[ind] = quad(funct_js, -np.pi/2, np.pi/2,
                                     args=(mx, r, d))

from scipy import odr

# Using the second order polynomial model
poly_model = odr.polynomial(2)
data = odr.Data(arr_mx, arr_js)
odr_obj = odr.ODR(data, poly_model)

# Running ODR fitting
output = odr_obj.run()

poly = np.poly1d(output.beta[::-1])
poly_y = poly(arr_mx)

poly

poly1d([-1.99369472e-01, -1.55978040e-06,  6.91704242e-01])

В классе numpy.poly1d:

class numpy.poly1d(c_or_r, r=False, variable=None)[source]

A one-dimensional polynomial class. The polynomial’s coefficients, in decreasing powers, or if the value of the second parameter is True, the polynomial’s roots (values where the polynomial evaluates to 0). For example, poly1d([1, 2, 3]) returns an object that represents \(x^2+2x+3\).

plt.figure(figsize=(8, 5))
plt.scatter(arr_mx, arr_js, edgecolor="red", s=5, label="Input data")
plt.plot(arr_mx, poly_y, label="polynomial ODR")

plt.xlabel("$m$ ")
plt.ylabel("$j_{s}$")

plt.title("Зависимость $j_s$  от параметра $m_x$")
plt.legend()

plt.show()

Многочлен восьмой степени \(P_8\)

# Using the 8th order polynomial model
poly_model = odr.polynomial(8)
data = odr.Data(arr_mx, arr_js)
odr_obj = odr.ODR(data, poly_model)

# Running ODR fitting
output = odr_obj.run()

poly = np.poly1d(output.beta[::-1])
poly_y = poly(arr_mx)

poly

poly1d([ 9.89331098e-03, -1.88713449e-06, -4.03163742e-02,  3.12929108e-06,
        1.00084081e-01, -1.42969838e-06, -2.61794136e-01,  1.37476617e-07,
        6.97143400e-01])

plt.figure(figsize=(8, 5))
plt.scatter(arr_mx, arr_js, edgecolor="red", s=5,  label="Input data")
plt.plot(arr_mx, poly_y, label="polynomial ODR")
plt.xlabel("$m$ ")
plt.ylabel("$j_{s}$")

plt.title("Зависимость $j_s$  от параметра $m_x$")
plt.legend(fontsize=12)

plt.show()

Вывод: Далее будем аппроксимировать интеграл \(I_y\) многочленами 8-ой степени.

Аналогично для интеграла \(I_x\)

# значения параметров
d = 0.8
r = 1.1
# массивы
Npoint = 1000
arr_mx = np.linspace(-1, 1, Npoint, endpoint=True)
arr_js = np.zeros(Npoint, dtype=np.float64)
arr_err = np.zeros(Npoint, dtype=np.float64)
# вычисление интегралов
for ind in range(Npoint):
    mx = arr_mx[ind]
    arr_js[ind], arr_err[ind] = quad(funct_Ix, -np.pi/2, np.pi/2,
                                     args=(mx, r, d))

# Using the 9th order polynomial model
poly_model_x = odr.polynomial(9)
data = odr.Data(arr_mx, arr_js)
odr_obj = odr.ODR(data, poly_model_x)

# Running ODR fitting
output = odr_obj.run()

poly = np.poly1d(output.beta[::-1])
poly_y = poly(arr_mx)

output.beta[::-1]

array([ 4.07228833e-02, -5.03280881e-06, -1.48956036e-01,  9.60432431e-06,
        2.67296946e-01, -5.85091919e-06, -3.74404776e-01,  1.27255573e-06,
        4.76585467e-01, -3.83898666e-08])

plt.figure(figsize=(8, 5))
plt.scatter(arr_mx, arr_js, edgecolor="red", s=5, label="Input data")
plt.plot(arr_mx, poly_y, label="polynomial ODR")
plt.xlabel("$m_x$")
plt.ylabel("$I_x$")

plt.title("Зависимость $I_x$  от параметра $m_x$")
plt.legend()

plt.show()

Вывод: Далее будем аппроксимировать интеграл \(I_x\) многочленом 9-ой степени.

Как отпределить точность аппроксимации?

2. Численное решение задачи Коши: библиотека SciPy

Задача Коши: Рассмотрим решение начальной задачи (Intial value problem) для системы обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно производной:

\( \begin{eqnarray} \begin{cases} \displaystyle \frac{dy(t)}{dt} = f(t,y(t)),\\ \displaystyle y|_{t=t_0} = y_0, \end{cases} \tag{1} \end{eqnarray} \)

где \(y=(y_1,...,y_n)^T\) - вектор-функция.

Пример 1: Численно решить задачу Коши:

\( \begin{eqnarray} \begin{cases} \displaystyle \frac{dy}{dt} = y\cos(t),\\ \displaystyle y(0)=y_0. \end{cases} \tag{2} \end{eqnarray} \)

Для сравнения приведем аналитическое решение задачи (2):

\[ y_{exact} = y_0 e^{\sin(t)}. \]

Воспользуемся библиотекой SciPy, содержащей функцию для решения начальной задачи:

scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, dense_output=False, events=None, vectorized=False, args=None, **options)[source]
Solve an initial value problem for a system of ODEs.

Для этого необходимо задать правые части уравнений (2).

from scipy.integrate import solve_ivp
from functools import partial

def F_right(t, y):
    ''' Определяет правую часть ДУ,
        примера 1'''
    return y*np.cos(t)

# Параметры численного счета
t0 = 0
tf = 10
nt = 1000
# Массив точек (сетка) в которых будет находится решение
t_e = np.linspace(t0, tf, nt)
# Начальное условие
y0 = np.array([3])

def y_exact(y0, t):
    ''' Определяет точное решение ДУ,
        примера 1'''
    return y0*np.exp(np.sin(t))

# Численное решение
sol_1 = solve_ivp(F_right, [t0, tf], y0, t_eval=t_e,
                  method='RK45', rtol=1e-8, atol=1e-8)

plt.figure(figsize=(8, 6))
plt.plot(sol_1.t, sol_1.y[0], label='Численное решение задачи (2) $y(t)$',
         linewidth=3.0)
plt.plot(t_e, y_exact(y0, t_e), label='Аналитическое решение $y_{exact}(t)$',
         linestyle='--', linewidth=3.0)
plt.xlabel('t', size=16)
plt.ylabel('$y(t)$', size=12)
plt.legend(loc='upper center', fontsize=11)
plt.show()

plt.figure(figsize=(8, 6))
plt.plot(t_e, np.abs(y_exact(y0, t_e)-sol_1.y[0]),
         label='Ошибка $|y_{exact}(t) - y(t)|$', linestyle='--', linewidth=3.0)
plt.xlabel('t', size=16)
plt.ylabel('$error(t)$', size=12)
plt.legend(fontsize=12)
plt.show()

Пример 2: Численно решить задачу Коши:

\( \begin{eqnarray} \begin{cases} \displaystyle \frac{dy}{dt} = y\cos(\omega t),\\ \displaystyle y(0)=y_0. \end{cases} \tag{3} \end{eqnarray} \)

Для сравнения приведем аналитическое решение задачи (3):

\[ y_{exact} = y_0 e^{\frac{1}{\omega}sin(\omega t)}. \]

Отметим, что в модель входит параметр \(\omega\). Для корректной передачи параметра в функцию SciPy воспользуемся методом:

from functools import partial

Модуль functools предназначен для функций высшего порядка: функций, которые воздействуют на другие функции или возвращают их. Для решения задачи:

• Зададим правые части уравнений (3);

• “Обернем” вызов решателя с помощью функции partial, для частичного применения функции, которое «замораживает» некоторую часть аргументов функции и/или ключевых слов.

def F_right2(t, y, omega):
    ''' Определяет правую часть ДУ примера 2
    omega - параметр'''
    return y*np.cos(omega*t)

# Параметр модели
omega = 5.  # np.pi/2
# Параметры численного счета
t0 = 0
tf = 10
nt = 1000
# Массив точек (сетка) в которых будет находится решение
t_e = np.linspace(t0, tf, nt)
# Начальное условие
y0 = np.array([3])

f = partial(F_right2, omega=omega)
t_e = np.linspace(t0, tf, nt)
sol_2 = solve_ivp(f, [t0, tf], y0, t_eval=t_e, method='RK45',
                  rtol=1e-8, atol=1e-8)

def y_exact2(y0, t, omega):
    ''' Определяет точное решение ДУ,
        примера 2'''
    if np.abs(omega) < np.finfo(type(omega)).eps:
        sol_ext = y0*np.exp(t)
    else:
        sol_ext = y0*np.exp(np.sin(omega*t)/omega)
    return sol_ext

plt.figure(figsize=(8, 6))
plt.plot(sol_2.t, sol_2.y[0], label='Численное решение задачи (3) $y(t)$',
         linewidth=3.0)
plt.plot(t_e, y_exact2(y0, t_e, omega),
         label='Аналитическое решение $y_{exact}(t) $',
         linestyle='--', linewidth=3.0)
plt.xlabel('t', size=16)
plt.ylabel('$y(t)$', size=12)
plt.legend(loc='upper center', fontsize=11)
plt.show()

# Задача на самостоятельное решение
@interact
def show_sol(omega=(0.1, 5.0, 0.1)):
    # Параметры численного счета
    t0 = 0
    tf = 10
    nt = 1000
    # Массив точек (сетка) в которых будет находится решение
    # Начальное условие
    y0 = np.array([3])

    f = partial(F_right2, omega=omega)
    t_e = np.linspace(t0, tf, nt)
    sol_2 = solve_ivp(f, [t0, tf], y0, t_eval=t_e, method='RK45',
                      rtol=1e-9, atol=1e-8)

    fig = plt.figure(figsize=(8, 6))
    plt.plot(t_e, sol_2.y[0],
             label='Численное решение задачи (3) $y(t)$',
             linewidth=3.0)
    plt.plot(t_e, y_exact2(y0, t_e, omega),
             label='Аналитическое решение $y_{exact}(t) $',
             linestyle='--', linewidth=3.0)
    plt.xlabel('t')
    plt.ylabel('$y(t)$')
    plt.legend(loc='upper right')
    plt.show()

Математическое моделирование джозефсоновского перехода сверхпроводник/ферромагнетик/сверхпроводник на поверхности трехмерного топологического изолятора

Аномальный эффект Джозефсона, который заключается в возникновении фазового сдвига в токфазовом соотношении гибридных джозефсоновских структур, состоящих из сверхпроводников и магнетиков приводит к возникновении конечного сверхпроводящего тока при нулевой джозефсоновской разности фаз. Данный фазовый сдвиг пропорционален намагниченности ферромагнетика и отражает совместное проявление сверхпроводимости и магнетизма.

Одной из возможных подобных гибридных структур является джозефсоновский переход сверхпроводник/ферромагнетик/сверхпроводник на поверхности трехмерного топологического изолятора, содержащего дираковские квазичастицы, в котором сильная зависимость энергии Джозефсона от ориентации намагниченности открывает новые возможности для контроля намагниченности джозефсоновским током или джозефсоновской фазой. Помимо наличия сдвига фазы, также в этой структуре джозефсоновский критический ток сильно зависит от ориентации намагниченности, а именно от составляющей намагниченности в плоскости вдоль направлении тока. Такая зависимость критического тока может привести к четырехкратному вырожденному состоянию ферромагнетика, которая резко контрастирует с обычным двукратным вырожденным состояниям. Активный интерес к исследованию таких структур вызван возможностью их практического приложения. Возникающая связь между магнитным и сверхпроводниковыми степенями свободы дает возможность взаимного контроля, т.е. управления магнитными свойствами посредством сверхпроводящего тока или наоборот.

Теоретическая модель

Рассмотрим S/F/S структуру, где два обычных s-волновых сверхпроводника и ферромагнетик, нанесенные на поверхность 3D TI, образуют джозефсоновский переход. Схематический вид такого перехода представлен на Рис.1.

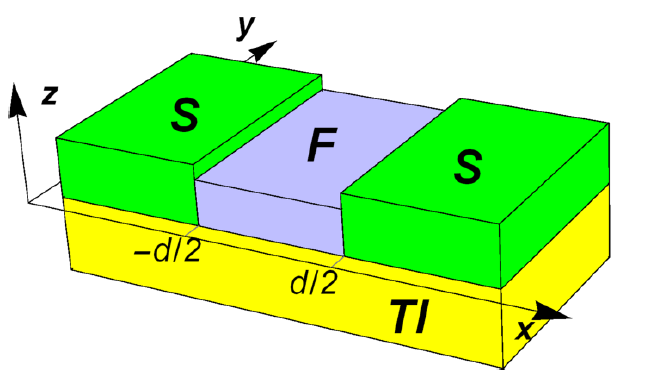
Рис.1. Схема S/F/S джозефсоновского перехода на поверхности 3D топологического изолятора. Легкая ось ферромагнетика направлена вдоль оси \(y\).

Ток-фазовое соотношение этого перехода задается выражением

\[ \begin{eqnarray} j_{s}=j_{c}\sin(\varphi-\varphi_{0}), \tag{1} \end{eqnarray} \]

где \(j_c\) - критический ток, \(\varphi\) - джозефсоновская разность фаз, \(\varphi_{0}=r m_{y}\) - аномальный сдвиг фазы, \(m_{y}=M_{y}/M_{s}\) - \(y\) компонента намагниченности (\(M_{y}\)) нормированная на намагниченность насыщения \(M_s\), \(r = 2 d h_{\text{exc}} / \upsilon_F\) - безразмерный параметр, определяющий величину спин-орбитального взаимодействия, \(d\) - толщина ферромагнитного барьера, \(h_{\text{exc}}\) - обменное поле, \(\upsilon_F\) -скорость Ферми.

Отличительной чертой рассматриваемого джозефсоновского перехода является то, что критический ток сильно зависит от ориентации намагниченности, а именно, от \(x\) компоненты намагниченности в плоскости вдоль направления тока и задается выражением

\[ \begin{eqnarray} j_c = j_b \int \limits_{-\pi/2}^{\pi/2}\cos\varphi\exp\left(-\frac{\tilde{d}}{\cos\phi}\right)\cos(r m_x\tan\varphi)d\varphi, \tag{2} \end{eqnarray} \]

где \(\varphi\) - угол между направлением квазичастичного тока и осью \(x\), \(m_{x}=M_{x}/M_{s}\) - \(x\) компонента намагниченности нормированная на \(M_s\), \(j_b = \frac{e\upsilon_F N_F\triangle^{2}}{\pi^{2}T}\), \(\triangle\) - сверхпроводящий параметр порядка, \(T\) - температура, \(N_F\) - концентрация частиц вблизи уровня Ферми, \(\upsilon_F\) - скорость Ферми, \(\tilde{d}\) - безразмерная длина контакта.

Динамика вектора намагниченности \(\mathbf{M}\) ферромагнитного слоя описывается в рамках уравнения Ландау - Лифшица - Гильберта (ЛЛГ):

\[ \begin{eqnarray} \frac{d \mathbf{M}}{d t} = -\gamma \mathbf{M} \times \mathbf{H}_{\text{eff}} + \frac{\alpha}{M_s} \mathbf{M}\times \frac{d \mathbf{M}}{d t}, \tag{3} \end{eqnarray} \]

где \(\gamma\) - гиромагнитное отношение, \(\alpha\) - гильбертовское затухание и \(\mathbf{H}_{\text{eff}}\) - эффективное поле. Эффективное поле определяется варьированием полной энергии системы по вектору намагниченности

\[ \begin{eqnarray} \mathbf{H}_{\text{eff}}=-\frac{1}{V_{F}}\frac{\delta E_{t}}{\delta \mathbf{M}}, \tag{4} \end{eqnarray} \]

где \(V_F\) - объем ферромагнитного слоя. Полная энергия системы состоит из энергии магнитной анизотропии

\[ \begin{eqnarray} E_{M}=-KV_{F}\bigg(\frac{M_{y}}{M_{s}}\bigg)^{2}, \tag{5} \end{eqnarray} \]

где \(K\) - константа анизотропии, и джозефсоновской энергии

\[ \begin{eqnarray} E_{J}=\frac{\Phi_{0} j_{c}S}{2\pi}[1-\cos(\varphi-rm_{y})], \tag{6} \end{eqnarray} \]

где \(\Phi_{0}\) - квант магнитного потока, \(S\) - площадь перехода.

Таким образом, компоненты эффективного поля в нормированных единицах могут быть записаны в виде:

\[\begin{split} \begin{eqnarray} h_{x}=\frac{H_{\text{eff,x}}}{H_F} &=& \frac{GrI_{x}}{j_{c0}} \left[1 - \cos\left(\varphi - rm_y\right)\right]\nonumber,\\ h_{y}=\frac{H_{\text{eff,y}}}{H_F} &=& \frac{GrI_{y}}{j_{c0}} \sin(\varphi - rm_y) + m_y\nonumber,\\ h_{z}=\frac{H_{\text{eff,z}}}{H_F} &=& 0\nonumber,\\ \tag{7} \end{eqnarray} \end{split}\]

где \(G = \Phi_0 j_b S/ 2 \pi K V_F\) - отношение амплитуды джозефсоновской энергии к магнитной, \(H_F = \omega_F/\gamma = K/M_s\), \(\omega_F\) - собственная частота ферромагнитного резонанса, а \(I_{x}\) и \(I_{y}\) интегральные выражения определяемые как:

\[\begin{split} \begin{eqnarray} I_{x} &=& \int\limits_{-\pi/2}^{\pi/2}\sin\phi\exp\bigg(-\frac{\tilde{d}}{\cos\varphi}\bigg)\sin(r m_{x}\tan\phi)d\varphi\nonumber,\\ I_{y} &=& \int\limits_{-\pi/2}^{\pi/2}\cos\phi\exp\bigg(-\frac{\tilde{d}}{\cos\varphi}\bigg)\cos(r m_{x}\tan\phi)d\varphi\nonumber.\\ \tag{8} \end{eqnarray} \end{split}\]

Здесь \(j_{c0}\) определяет выражение для критического тока при \(m_x = 0\) и записывается как

\[ \begin{equation} j_{c0}=\int\limits_{-\pi/2}^{\pi/2}\cos\phi\exp(-\frac{\tilde{d}}{\cos\phi})d\phi \tag{9} \end{equation} \]

Таким образом, в нормированных величинах, получим систему уравнений:

\[\begin{split} \begin{eqnarray} \frac{dm_{x}}{dt} &=& -\frac{\omega_{F}}{1+\alpha^2}\bigg((m_{y} h_{z}-m_{z} h_{y}) + \alpha [m_{x} (m_{x} h_{x}+m_{y} h_{y}+m_{z} h_{z})-h_{x} m^{2}]\bigg),\nonumber\\ \frac{dm_{y}}{dt} &=& -\frac{\omega_{F}}{1+\alpha^2}\bigg((m_{z} h_{x}-m_{x} h_{z}) +\alpha [m_{y} (m_{x} h_{x}+m_{y} h_{y}+m_{z} h_{z})-h_{y} m^{2}]\bigg),\nonumber\\ \frac{dm_{z}}{dt} &=& -\frac{\omega_{F}}{1+\alpha^2}\bigg((m_{x} h_{y} - m_{y} h_{x}) +\alpha [m_{z} (m_{x} h_{x}+m_{y} h_{y}+m_{z} h_{z})-h_{z} m^{2}]\bigg).\nonumber\\ \tag{10} \end{eqnarray} \end{split}\]

При заданном значении напряжении можно считать разоность фаз \(\varphi\) линейной функцией от времени, т.е. \(\varphi=Vt\). Тогда выражения для компонент эффективного поля записываются в виде

\[\begin{split} \begin{eqnarray} h_{x} &=& \frac{GrI_{x}}{j_{c0}} \left[1 - \cos\left(Vt - rm_y\right)\right], \\ h_{y} &=& \frac{GrI_{y}}{j_{c0}} \sin(Vt - rm_y) + m_y, \\ h_{z} &=& 0.\\ \tag{11} \end{eqnarray} \end{split}\]

Постановка задачи

Легкая ось намагниченности в ферромагнитном слое направлена вдоль оси \(y\), т.е. направления \(m_y=\pm1\) являются стабильными. В работе\cite{nashaat19prb} было показано, что в SFS джозефсоновском переходе на поверхности топологического изолятора при определенных значениях параметров модели реализуются четырехкратно вырожденные стабильные состояния намагниченности.

Наша задача заключается, в том чтобы на основе математического моделирования продемонстрировать реализацию этих вырожденных состояний.

Апроксимация интегралов

Отметим, что при численном решении системы дифференциальных уравнений приходится на каждом шаге по времени вычислить интегралы. Это сильно замедляет процесс решения уравнений. Эту проблему можно решить следующим образом:

1. Вычислить интегралы численно в интервале \(m_x \in [-1,1]\) с определенным шагом

2. Интерполировать полученный результат полиномом определенной степени

3. Затем вставить полученную приближенную формулу в уравнении и решать систему уравнений

%matplotlib inline

Задаем значения параметров модели для вычисления интегралов

d = 0.3
r = 0.5

Определяем подынтегральные функции

def funct_Ix(phi, mx, r, d):
    '''Defines the integrand in the definition of current Ix,
        mx, r, d - parameters'''
    return (np.sin(phi) * np.exp(-d / np.cos(phi)) * np.sin(r*mx*np.tan(phi)))

def funct_Iy(phi, mx, r, d):
    '''Defines the integrand in the definition of current Iy,
        mx, r, d - parameters'''
    return (np.cos(phi) * np.exp(-d / np.cos(phi)) * np.cos(r*mx*np.tan(phi)))

Создаем массивы для \(m_x\) и соответствующих значений интегралов

# массивы
Npoint = 1000
arr_mx = np.linspace(-1, 1, Npoint, endpoint=True)
arr_Ix = np.zeros(Npoint, dtype=np.float64)
arr_Iy = np.zeros(Npoint, dtype=np.float64)
arr_errx = np.zeros(Npoint, dtype=np.float64)
arr_erry = np.zeros(Npoint, dtype=np.float64)
# вычисление интегралов
for ind in range(Npoint):
    mx = arr_mx[ind]
    arr_Ix[ind], arr_errx[ind] = quad(funct_Ix, -np.pi/2, np.pi/2,
                                      args=(mx, r, d))
    arr_Iy[ind], arr_erry[ind] = quad(funct_Iy, -np.pi/2, np.pi/2,
                                      args=(mx, r, d))

Аппроксимация интегралов \(I_{x}\) и \(I_{y}\) многочленом девятой \(P_{9}\) и восьмой \(P_{8}\) степени соответственно

# Using 9th order polynomial model
poly_model = odr.polynomial(9)
data = odr.Data(arr_mx, arr_Ix)
odr_obj = odr.ODR(data, poly_model)

# Running ODR fitting
output = odr_obj.run()

Ixfit = np.poly1d(output.beta[::-1])

# using 8th order polynomial model
poly_model = odr.polynomial(8)
data = odr.Data(arr_mx, arr_Iy)
odr_obj = odr.ODR(data, poly_model)

# Running ODR fitting
output = odr_obj.run()

Iyfit = np.poly1d(output.beta[::-1])

Определение функции для \(j_{c0}\)

def jc0(d):
    '''Определяет функцию для критического тока при отсутсвии F слоя
    d - параметр модели'''
    result = quad(lambda phi: np.cos(phi)*np.exp(-d/np.cos(phi)),
                  -np.pi/2, np.pi/2)
    return result

Вычиcление \(j_{c0}\)

Jc0 = jc0(d)
J0 = Jc0[0]

Определяем правые части системы уравнений

def my_sfs(t, S, G, r, alpha, wF, d, V, J0):
    '''Определяет правые части ДУ
    G, r, alpha, wF - параметры модели
    S=[mx, my, mz, ph] - искомая вектор-функция'''
    mx = S[0]
    my = S[1]
    mz = S[2]

    Jx = Ixfit(mx)
    Jy = Iyfit(mx)

    Hx = (G*r*Jx/J0)*(1-np.cos(V*t-r*my))
    Hy = (G*r*Jy/J0)*np.sin(V*t-r*my)+my
    Hz = 0

    H = [Hx, Hy, Hz]
    M = [mx, my, mz]

    m2 = np.dot(M, M)
    HdM = np.dot(H, M)

    ksi = -wF/(1+alpha*alpha*m2)

    dmx = ksi * ((my*Hz-mz*Hy) + alpha * (mx*HdM-Hx*m2))
    dmy = ksi * ((mz*Hx-mx*Hz) + alpha * (my*HdM-Hy*m2))
    dmz = ksi * ((mx*Hy-my*Hx) + alpha * (mz*HdM-Hz*m2))

    dS = [dmx, dmy, dmz]
    return dS

Проверяем на работоспособность

s = np.array([0, 1, 0])
dS = my_sfs(0, s, 4.12, 0.5, 0.01, 1, 0.3, 5, J0)
dS

[-3.9161076125833644e-10, -0.0, -3.9161076125833646e-08]

G = 4.5
r = 0.5
d = 0.3
wF = 1
alpha = 0.01
V = 5

t0 = 0
tf = 1500
nt = 15000

Задаем начальные условия

mx0 = -0.5
mz0 = 0
my0 = np.sqrt(1-mx0*mx0-mz0*mz0)

Численное решение системы уравнений

f = partial(my_sfs, G=G, r=r, alpha=alpha, wF=wF, d=d, V=V, J0=J0)
t_e = np.linspace(t0, tf, nt)
s0 = np.array([mx0, my0, mz0])
sol_1 = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='BDF',
                  rtol=1e-8, atol=1e-8)

plt.figure(figsize=(18, 6))
plt.subplot(1, 3, 1)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[0], label='Компонента $m_x $', color='b')
plt.xlabel('t', size=16)
plt.ylabel('$m_{x}$', size=16)
plt.legend(fontsize=12)
plt.subplot(1, 3, 2)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[1], label='Компонента $m_y $', color='g')
plt.xlabel('t', size=16)
plt.ylabel('$m_{y}$', size=16)
plt.legend(fontsize=12)
plt.subplot(1, 3, 3)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[2], label='Компонента $m_z $', color='r')
plt.xlabel('t', size=16)
plt.ylabel('$m_{z}$', size=16)
plt.legend(fontsize=12)
plt.show()

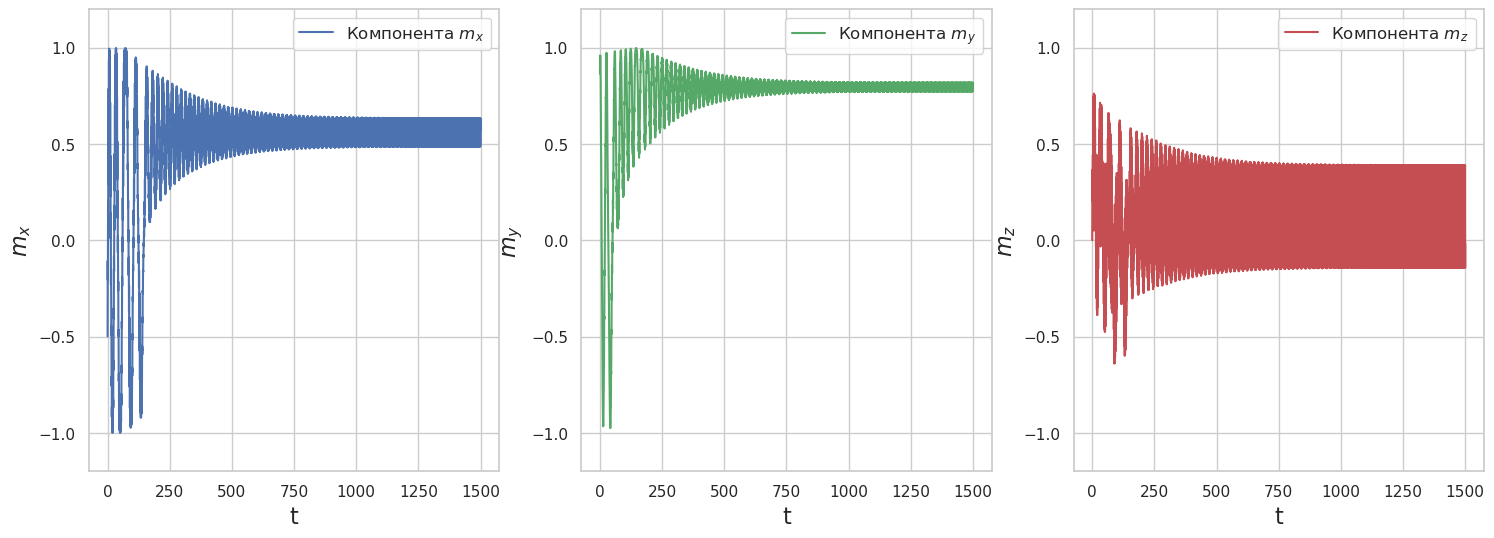
Влияние начальных условий

mx0 = 0.5
mz0 = 0
my0 = np.sqrt(1-mx0*mx0-mz0*mz0)

f = partial(my_sfs, G=G, r=r, alpha=alpha, wF=wF, d=d, V=V, J0=J0)
t_e = np.linspace(t0, tf, nt)
s0 = np.array([mx0, my0, mz0])
sol_1 = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='BDF',
                  rtol=1e-8, atol=1e-8)

plt.figure(figsize=(18, 6))
plt.subplot(1, 3, 1)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[0], label='Компонента $m_x $', color='b')
plt.xlabel('t', size=16)
plt.ylabel('$m_{x}$', size=16)
plt.legend(fontsize=12)
plt.subplot(1, 3, 2)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[1], label='Компонента $m_y $', color='g')
plt.xlabel('t', size=16)
plt.ylabel('$m_{y}$', size=16)
plt.legend(fontsize=12)
plt.subplot(1, 3, 3)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[2], label='Компонента $m_z $', color='r')
plt.xlabel('t', size=16)
plt.ylabel('$m_{z}$', size=16)
plt.legend(fontsize=12)
plt.show()

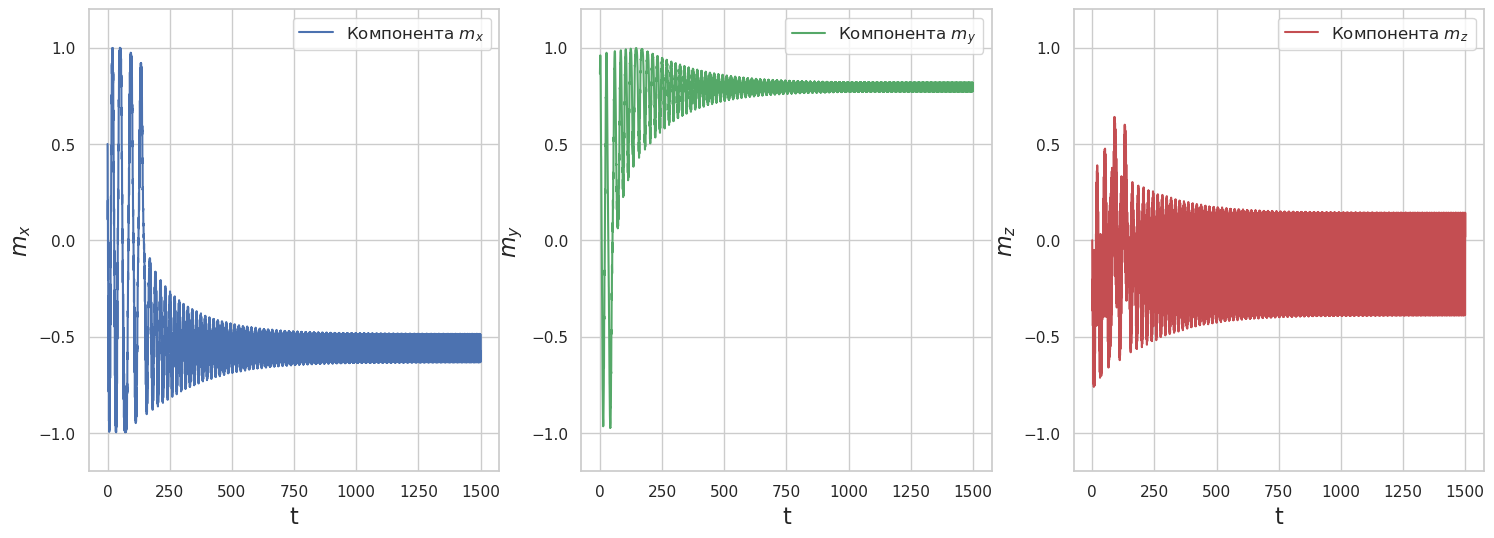
Влияние параметра \(G\)

G = 1

mx0 = -0.5
mz0 = 0
my0 = np.sqrt(1-mx0*mx0-mz0*mz0)

f = partial(my_sfs, G=G, r=r, alpha=alpha, wF=wF, d=d, V=V, J0=J0)
t_e = np.linspace(t0, tf, nt)
s0 = np.array([mx0, my0, mz0])
sol_1 = solve_ivp(f, [t0, tf], s0, t_eval=t_e, method='BDF',
                  rtol=1e-8, atol=1e-8)

plt.figure(figsize=(18, 6))
plt.subplot(1, 3, 1)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[0], label='Компонента $m_x $', color='b')
plt.xlabel('t', size=16)
plt.ylabel('$m_{x}$', size=16)
plt.legend(fontsize=12)
plt.subplot(1, 3, 2)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[1], label='Компонента $m_y $', color='g')
plt.xlabel('t', size=16)
plt.ylabel('$m_{y}$', size=16)
plt.legend(fontsize=12)
plt.subplot(1, 3, 3)
plt.ylim(-1.2, 1.2)
plt.plot(sol_1.t, sol_1.y[2], label='Компонента $m_z $', color='r')
plt.xlabel('t', size=16)
plt.ylabel('$m_{z}$', size=16)
plt.legend(fontsize=12)
plt.show()

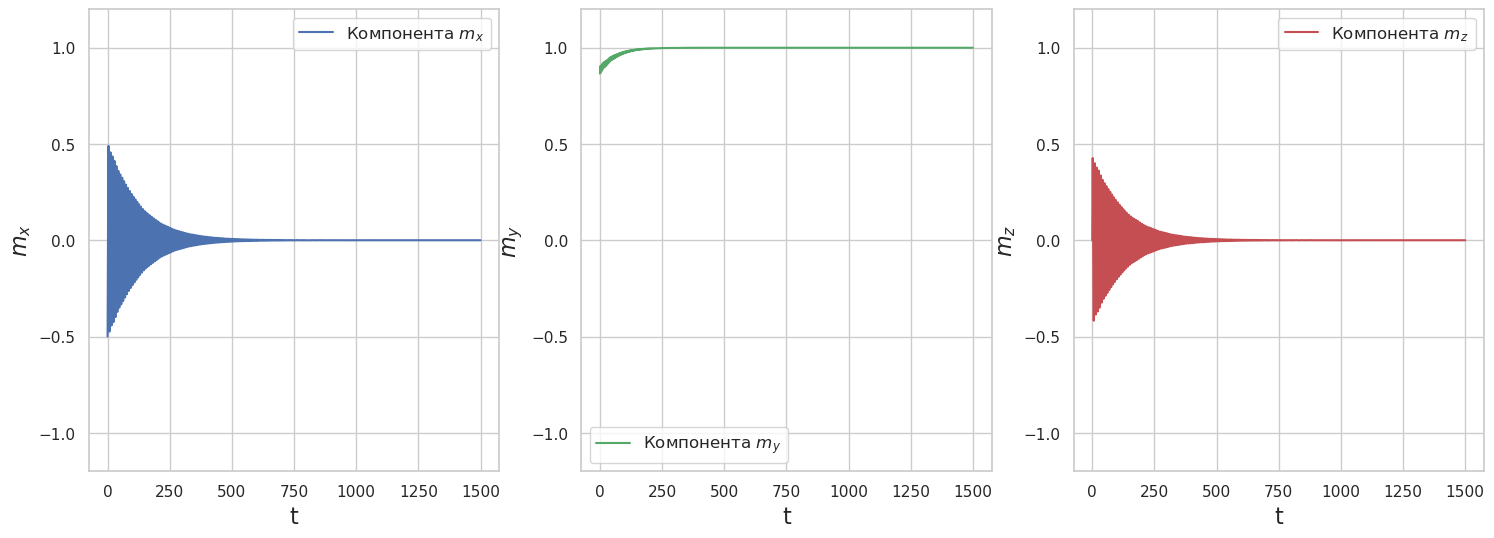
Задача для хакатона

Исследовать зависимость реализуемых стабильных состояний от параметра \(G\)

Алгоритм:

1. При заданных начальных условий и фиксированного значения \(G\) решить систему уравнений в интервале \([0,t_{max}]\).

2. Построить графики \(m_x\), \(m_y\), \(m_z\) от \(t\) определить значение времени \(t_s\) (time of stabilization), после которого решения стабилизируются.

3. Усреднить полученные \(m_x\), \(m_y\), \(m_z\) в интервале \([t_s,t_{max}]\).

4. Построить зависимость средних \(<m_x>\), \(<m_y>\), \(<m_z>\) от \(G\), где анализируя эти зависимости можно говорить о реализации того или иного стабильного состояния.

5. Разработать параллельную реализацию алгоритма для вычисления зависимости средних \(<m_x>\), \(<m_y>\), \(<m_z>\) от \(G\).