Python-реализация алгоритмов и инструментарий для моделирования динамики сверхпроводникого квантового интерферометра с двумя джозефсоновскими переходами (Вычисление зависимости величины тока возврата и модуляции напряжения от величины внешнего магнитного поля)#
1. Описание модели#
Эффект Джозефсона и джозефсоновский переход:
Связь двух сверхпроводящих слоев посредством тонкого слоя несверхпроводящего барьера образует структуру называемую джозефсоновским переходом (в честь Английского ученого Брайана Джозефсона). При пропускании электрического тока через джозефсоновский переход в зависимости от величины тока наблюдается стационарный и нестационарный эффект Джозефсона.
Стационарный эффект Джозефсона. При пропускании тока ниже критического значения (\(I<I_{c}\)) в джозефсоновском переходе (ДП) отсутсвует напряжение и через переход течет сверхпроводящий ток. Данный ток пропорционален синусу разности фаз параметров порядка сверхпроводящих слоев образующих ДП.
Нестационарный эффект Джозефсона. При увеличении тока выше критического значения (\(I>I_{c}\)) возникает переменное напряжение в ДП и оно пропорционально производной разности фаз
Сверхпроводниковые квантовые интерференционные устройства (СКВИД)
Системы содержащие джозефсоновские переходы давно нашли свое применение в различных отраслях науки и техники. Одним из таких примеров является так называемые сверхпроводниковые квантовые интерференционные устройства. В литературе эти устройства известны как СКВИД (от английского SQUID - Superconducting Quantum Interference Device). Различают двух типов СКВИДа: СКВИД постоянного тока (DC-SQUID) и СКВИД переменного тока (RF-SQUID). СКВИД постоянного тока представляет собой сверхпроводниковое кольцо, состоящее из двух параллельно соединенных джозефсоновских переходов, и широко применяется как устройство для измерения очень слабых магнитных полей. А СКВИД переменного тока применяются как чувствительный прибор слабого переменного поля.
Рассмотрим, СКВИД постоянного тока (DC-SQUID), схематический вид которого представлен на Рис.1. Плоскость на которой лежат джозефсоновские переходы и ограничено соединяющими сверхпроводящими проводниками будем называть поверхностью СКВИДа. Предположим, что перпендикулярно к поверхности СКВИДа приложено постоянное магнитное поле \(B\) направленное снизу вверх и оно приведет к потоку \(\Phi_{ext}=BS\), где \(S\) площадь поверхности СКВИДа.
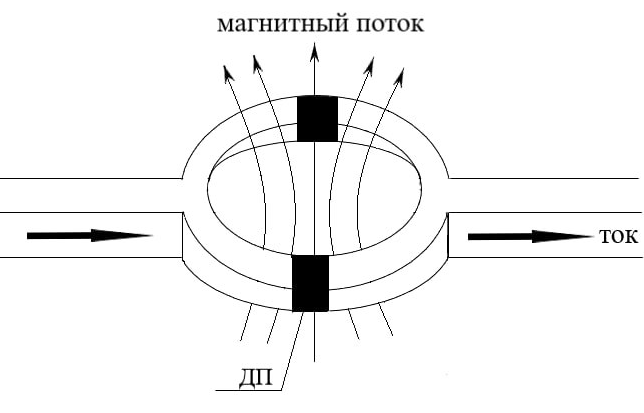
Рис.1 Схематический вид СКВИДа
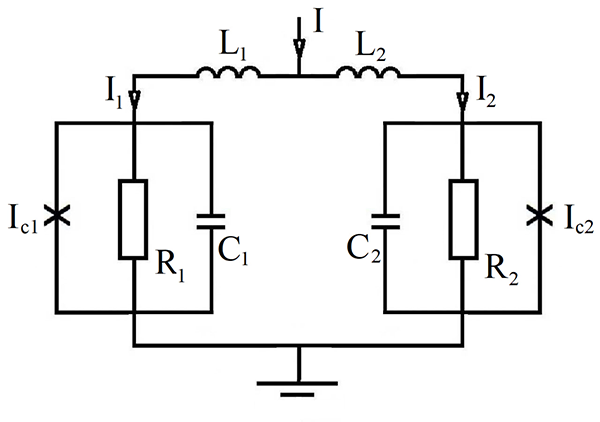
Рис.2 Эквивалентная схема СКВИДа.
Динамика перехода описывается Resitively Capasitevily Shunted Junction (RCSJ) моделью\cite{r}. В рамках этой модели ДП моделируется как параллельное соединение конденсатора, резистора и сверхпроводника, через которые протекают, соответственно, ток смещения, квазичастичный и сверхпроводящий токи. Учитывая индуктивности сверхпроводящих проводников соединяющие джозефсоновские переходы 1 и 2 Можно написать эквивалентную схему СКВИДа, которая представлена на Рис. 2. Индексами 1 и 2 обозначены, соответсвенно левый и правый и правый ДП. Через СКВИД пропускается внешный ток \(I\), которая распределясь на \(I_{1}\) и \(I_{2}\) течет через джозефсоновские переходы 1 и 2 и в резистивном состоянии ДП-ов приводит к среднему напряжению \(V\). Кроме того из за наличия потока внешнего магнитного поля \(\Phi_{ext}\) возникает циркулирующий сверхпроводящий ток \(J\). Здесь \(L_{1}\) и \(L_{2}\) обозначают индуктивность сверхпроводящих проводников соединяющих джозефсоновские переходы и \(C_{1,2}\), \( R_{1,2}\), \( I_{c,1,2}\) емкость, сопротивление и критический ток ДП, соответвенно. Согласно RCSJ-модели токи \(I_{1}\) и \(I_{2}\) определяются выражениями
где \(V_{i}=\frac{\Phi_{0}}{2\pi}\frac{d\varphi_{i}}{dt}\) напряжение в \(i\)-ом переходе, \(\Phi_{0}=\frac{\hbar}{2e}\)-квант магнитного потока. С другой стороны, согласно правила Кирхгофа для токов можно записать
Далее для простоты предполагаем, что индуктивности проводников равны друг другу и ДП СКВИДа одинаковы, т.е. полагаем
Магнитный поток через СКВИД складывается из потока создаваемого внешним полем \(\Phi_{ext}\) и циркулирующим током \(J\) и записывается в виде
Хорошо известно, что магнитный поток через сверхпроводниковые контуры квантуется, т.е. принимает дискретное значения кратное к \(\Phi_{0}\). Выражение для квантования магнитного потока для рассматриваемой системы можно записать
или
где \(\varphi_{ext}\) безразмерный поток внешнего магнитного поля нормированный на \(\Phi_{0}\). Отсюда можно получить выражению для циркулирующего тока
Тогда с учетом (2)-(5) можно получить замкнутую систему уравнений для описания СКВИДа:
Переходя к безразмерным величинам можно написать
где \(\beta_{c}=C\Phi_{0}\omega_{c}^{2}/(2\pi I_{c})\) - параметр МакКамбера, \(\omega_{c}=2\pi R I_{c}/\Phi_{0}\)- характеристическая частота Джозефсона, \(\beta_{L}=2\pi L I_{c}/\Phi_{0}\)- обезразмеренная индуктивность, \(\Phi_{0}=h/(2e)\) - квант магнитного потока, \(\varphi_{ext}=\Phi_{ext}/\Phi_{0}\) - безразмерный поток внешнего магнитного поля. Здесь напряжение нормировано на \(V_{c}=I_{c}R\), ток на \(I_{c}\) и время \(t\) на \(\omega^{-1}_{c}\), где \(\omega_{c}=2\pi V_{c}/\Phi_{0}\). Начальные условия для системы уравнений \eqref{eqsystem} заданы в виде \(V_1(0)=V_2(0)=0\) и \(\varphi_1(0)=\varphi_2(0)=0\).
Постановка задачи: Необходимо вычислить:
Вольт-амперную характеристику (ВАХ) СКВИДа
Зависимость критического тока от потока внешнего магнитного поля.
Алгоритм рассчета
Ниже опишем алгоритм вычисления ВАХ и зависимости критического тока от внешнего магнитного поля. При заданном значений параметров и начальных условий при фиксированном значении тока \(I\) численно решается СДУ (\ref{eqsystem}) в интервале времени [0, Tmax] с шагом \(\Delta t\). Полученная временная зависимость напряжения усредняется по времени по формуле
и в результате вычисляется одна точка ВАХ для заданного значения \(I\). Отметим, что при усреднении интегрирования начинается от времени \(Tmin\), после которого решение стабилизируется. Далее меняется значение тока на δI и повторяется вышеописанные действия. При этом вычисленные φ(Tmax) и V (Tmax) для предыдущего значения тока будут использоваться в качестве начального условия для текущего значения тока. Таким образом увеличивая ток до Imax и уменьшая его обратно до нуля получаем ВАХ ДП.
Для определения критического тока в процессе вычисления ВАХ фиксируется значения внешнего тока при которой выполняется условие V>0, т е значение тока при которой возникает напряжение, считается критическим током.
Подключаем библиотеки#
import numpy as np
import matplotlib.pyplot as plt
import math as m
from scipy.integrate import solve_ivp
from functools import partial
from scipy.integrate import odeint
import time
from numbalsoda import lsoda_sig, lsoda, dop853
from numba import njit, cfunc
import seaborn as sns
sns.set()
sns.set(style="whitegrid")
%matplotlib inline
1. Численное решение задачи Коши для системы уравнений#
Функция для вычисления значений правых частей уравнений (Numba version)#
@cfunc(lsoda_sig)
def rhs(t, S, dS, p):
''' Функция определяющая правую часть систему уравнений.
Возвращает значения правой части уравнений при заданных значениях
параметров.
S - массив математических функций
dS - массив производных от математических функций по времени
p - массив параметров
'''
# Задаем параметров модели
beta_c = p[0]
beta_L = p[1]
Pi = p[2]
n = p[3]
Icurr = p[4]
ph_ext = p[5]
# S массив которая содержит значения функций в начале (начальное условие)
ph1 = S[0]
V1 = S[1]
ph2 = S[2]
V2 = S[3]
# Задаем правую часть системы уравнений
dph1 = V1
dV1 = (1./beta_c) * ((Icurr/2.) - V1 - np.sin(ph1)
+ (1./(2.*beta_L)) * (ph2-ph1+2*Pi*(n-ph_ext)))
dph2 = V2
dV2 = (1./beta_c) * ((Icurr/2.) - V2 - np.sin(ph2)
- (1./(2.*beta_L)) * (ph2-ph1+2*Pi*(n-ph_ext)))
# Передаем правые части уравнений в массив dS
dS[0] = dph1
dS[1] = dV1
dS[2] = dph2
dS[3] = dV2
funcptr = rhs.address # address to ODE function
Задаем значения параметров модели для численного решения системы уравнений#
Важно: необходимо соблюдать типы переменных, когда задаем начальные условия и параметры
beta_c = 0.1 # Параметр диссипации
beta_L = 1.0 # Амплитуда внешнего излучения
Pi = 3.14159265358979323
n = 0 # Период внешнего излучения
Icurr = 2.7
ph_ext = 0.5
Tmax = 800 # Максимальное значение времени
deltat = 0.05
t0 = 0
nt = int(Tmax / deltat)
Imax = 2.7
Создаем массив с значениями времени для решения уравнения и задаем начальные условия
time_array = np.linspace(0, Tmax, num=nt)
s0 = np.array([0, 0, 0, 0]) # Initial conditions
Создаем массив с значениями параметров
# beta_c, beta_L, Pi, n, Icurr, ph_ext
data = np.array([beta_c, beta_L, Pi, n, Icurr, ph_ext])
data
array([0.1 , 1. , 3.14159265, 0. , 2.7 ,
0.5 ])
Численно решаем систему уравнений методом LSODA
%%time
# integrate with lsoda method
usol, success = lsoda(funcptr, s0, time_array, rtol = 1e-8, atol = 1e-8, data = data)
CPU times: user 154 ms, sys: 3.94 ms, total: 158 ms
Wall time: 158 ms
Извлекаем из массива решений значения напряжения V1 и V2
V1time = usol[:, 1]
V2time = usol[:, 3]
Временная зависимость V1 и V2
fig = plt.figure(figsize=(12, 10))
plt.plot(time_array, V1time, label='Временная зависимость', linewidth=2)
plt.xlabel('time', size=12)
plt.ylabel('V1', size=12)
plt.legend(loc='upper right')
plt.show()
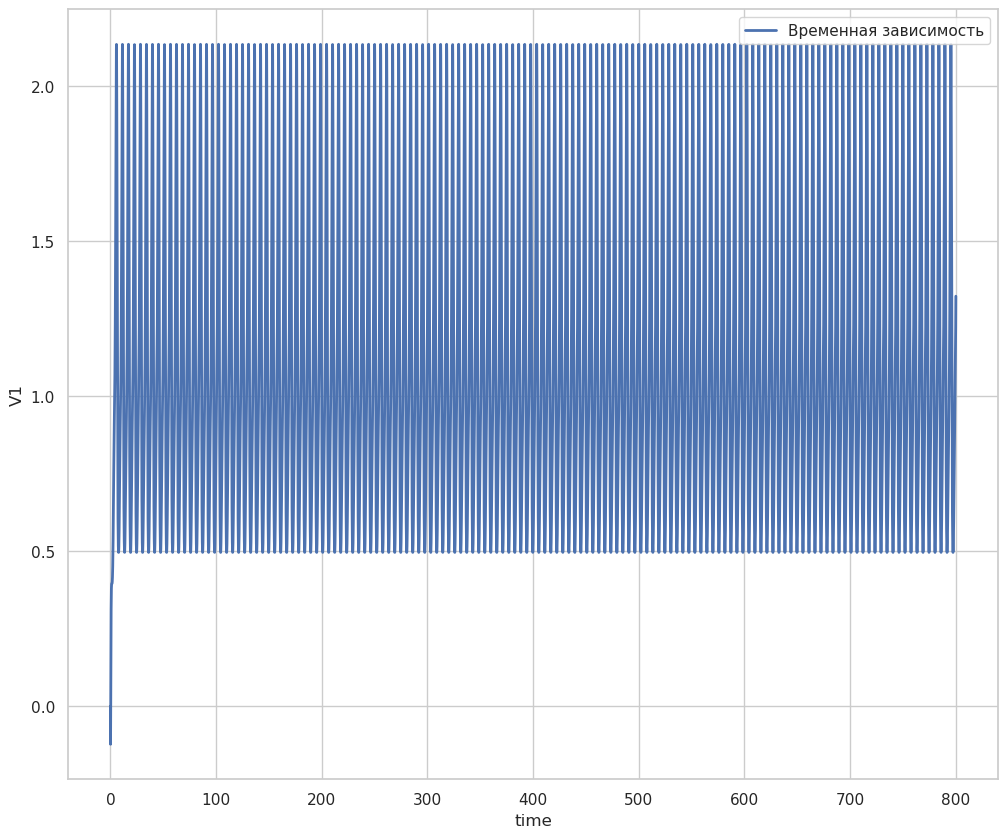
fig = plt.figure(figsize=(12, 10))
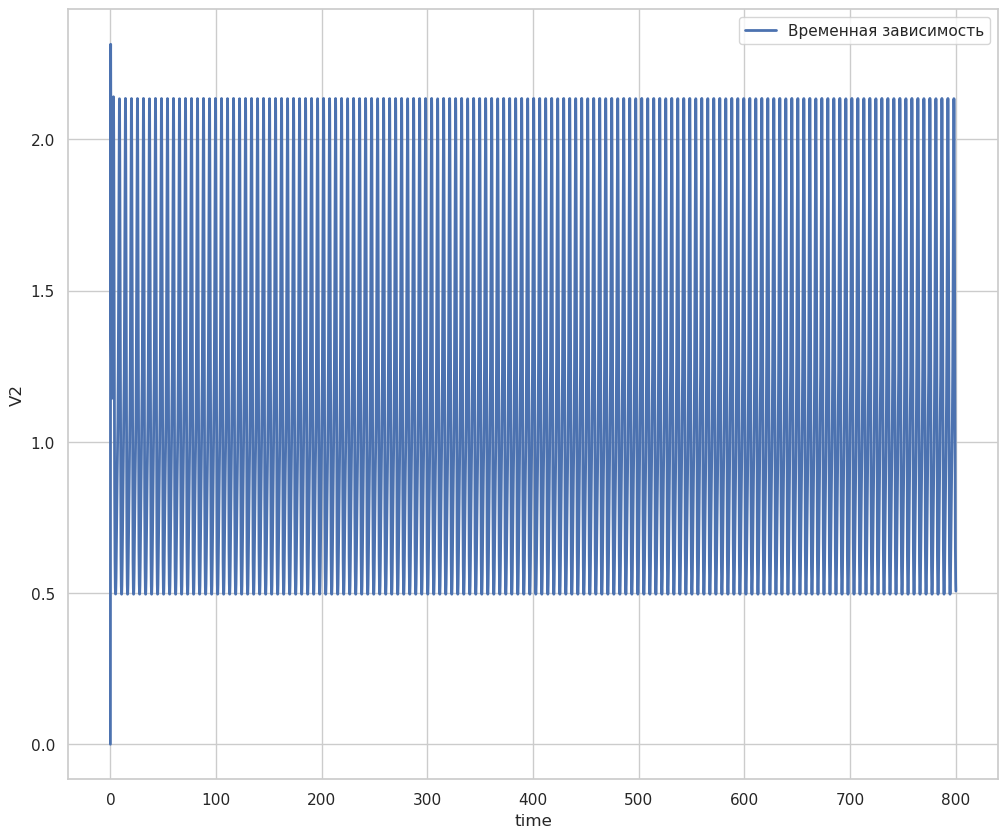
plt.plot(time_array, V2time, label='Временная зависимость', linewidth=2)
plt.xlabel('time', size=12)
plt.ylabel('V2', size=12)
plt.legend(loc='upper right')
plt.show()
2. Алгоритм для нахождения вольт-амперной характеристики (ВАХ) СКВИДа#
Для нахождения ВАХ нам нужно полученную временную зависимость усреднить. Для этого необходимо усреднить по отдельности V1 и V2 и затем вычислить среднее от полученных < V1 > и < V2 >. Этот шаг можно реализовать в виде функции которая принимая временные зависимости V1 и V2 возвращает среднее значения < V >
@njit
def averageV_new(ntmin, nt, deltat, V1, V2):
''' Функция для вычисления среднего значения напряжения.
Возвращает среднее значение напряжения для заданной
временной зависимости напряжений в первом и втором ДП
ntmin-номер шага по времени соответсвующая
нижней границе интегрирования,
nt - количество точек по времени, в которых найдены решения,
V1 - временная зависимость напряжения первого ДП,
V2 - временная зависимость напряжения второго ДП,
'''
V1av = np.sum(V1[ntmin: nt])/((nt-ntmin))
V2av = np.sum(V2[ntmin: nt])/((nt-ntmin))
Vav = (V1av + V2av)/2
return Vav
Функция для вычисления одной точки ВАХ
Создаем функцию, которая вычисляет одну точку ВАХ, т.е. выполняет следующие шаги:
принимает начальные условия и значения параметров модели
решает численно уравнения
используя ранее созданную функцию averageV_new усредняет напряжение
возвращает среднее напряжение и начальные условия для вычисления следующей точки ВАХ
@njit
def cvcpoint_new(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat):
''' Функция для вычисления одной точки ВАХ.
Возвращает для заданного значения тока вычисленную среднее значение
напряжения при заданных значений параметров.
s0 - массив начальных условий,
beta_c, beta_L, Pi, n, Icurr, ph_ext,-параметры модели
nt - количество точек по времени, в которых найдены решения,
ntmin - номер шага по времени соответсвующее
нижней границе интегрирования,
t0 - начальное значение времени,
deltat - шаг по времени
'''
data = np.array([beta_c, beta_L, Pi, n, Icurr, ph_ext])
t_e = np.linspace(t0, nt*deltat, nt)
# integrate with lsoda method
usol, success = lsoda(funcptr, s0, t_e, rtol=1e-8, atol=1e-8, data=data)
# получение результатов из массива usol
ph1time = usol[:, 0]
V1time = usol[:, 1]
ph2time = usol[:, 2]
V2time = usol[:, 3]
s0 = np.array([ph1time[nt-1], V1time[nt-1], ph2time[nt-1], V2time[nt-1]])
Vav = averageV_new(ntmin, nt, deltat, V1time, V2time)
return np.array([Vav, ph1time[nt-1], V1time[nt-1],
ph2time[nt-1], V2time[nt-1]])
Функция для вычисления ВАХ
@njit
def comput_vax(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat, a, deltaI):
''' Функция для вычисления однопетлевой ВАХ.
Возвращает для заданного значения параметров массива
с значениями тока и вычисленного напряжения
s0 - массив начальных условий,
beta_c, beta_L, Pi, n, Icurr, ph_ext,-параметры модели
nt - количество точек по времени, в которых найдены решения,
ntmin - номер шага по времени соответсвующее
нижней границе интегрирования,
t0 - начальное значение времени,
deltat - шаг по времени
deltaI - шаг по току
'''
Vplot = []
Iplot = []
while Icurr < 100:
res = cvcpoint_new(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat)
Vav = res[0]
s0 = res[1:]
Vplot.append(Vav)
Iplot.append(Icurr)
Icurr += a*deltaI
if(Icurr > Imax):
a = -1
if ((Icurr < 0) and (a == -1)):
break
return np.column_stack((np.array(Iplot), np.array(Vplot)))
Задаем значения параметров для вычисления ВАХ
Tmin = 50.0 # Начало интервала для интегрирования для усреднения
ntmin = int(Tmin/deltat)
deltaI = 0.001
Icurr = 0.0
a = 1
Imax = 2.2
s0 = np.array([0.0, 0.0, 0.0, 0.0])
res = cvcpoint_new(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat)
print(res)
[-7.81324927e-13 -8.31711194e-01 -2.12310771e-13 8.31711194e-01
-2.02754355e-13]
print(res[0])
-7.813249272940803e-13
print(res[1:])
[-8.31711194e-01 -2.12310771e-13 8.31711194e-01 -2.02754355e-13]
Вычислим ВАХ
start = time.time()
res = comput_vax(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat, a, deltaI)
end = time.time()
print(end-start)
27.4161536693573
График ВАХ
fig = plt.figure(figsize=(12, 10))
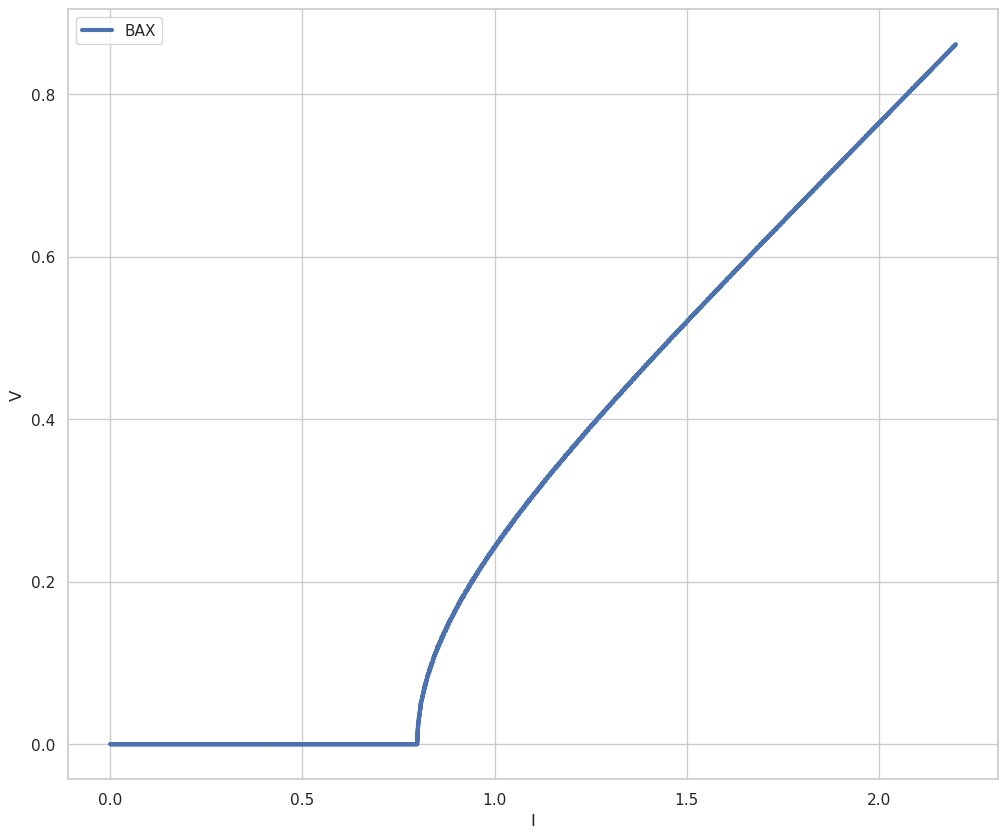
plt.plot(res[:, 0], res[:, 1], label='ВАХ', linewidth=3.0)
plt.xlabel('I', size=12)
plt.ylabel('V', size=12)
plt.legend(loc='upper left')
plt.show()
Описание ВАХ#
Как видно из ВАХ с увеличением тока начиная от нуля до 0.8 значения напряжение равна нулю (стационарный эффект Джозефсона). При достижении значения тока 0.8 появляется напряжение и далее с ростом тока растет и напряжение. Как было отмечено в описании модели ток при котором появляется напряжение назывется критическим током. Теперь рассмотрим как критический ток меняется с изменением внешнего потока.
Исследование влияния \(\varphi_{ext}\) на ВАХ#
Проведем вычисления при различных значений \(\varphi_{ext}\), например при \(\varphi_{ext}=0\), \(\varphi_{ext}=0.25\) и \(\varphi_{ext}=0.5\). Численное моделирование проводилось в интервале времени [0, 1000] с шагом 0.05.
ph_ext = 0
start = time.time()
res0 = comput_vax(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat, a, deltaI)
end = time.time()
print(end-start)
6.295086145401001
ph_ext = 0.25
start = time.time()
res1 = comput_vax(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat, a, deltaI)
end = time.time()
print(end-start)
13.635685443878174
ph_ext = 0.5
start = time.time()
res2 = comput_vax(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat, a, deltaI)
end = time.time()
print(end-start)
26.87863850593567
График ВАХ#
fig = plt.figure(figsize=(9, 8))
plt.plot(res0[:, 0], res0[:, 1], label='ВАХ phi_ext=0', linewidth=3.0)
plt.plot(res1[:, 0], res1[:, 1], label='ВАХ phi_ext=0.25', linewidth=3.0)
plt.plot(res2[:, 0], res2[:, 1], label='ВАХ phi_ext=0.5', linewidth=3.0)
plt.xlabel('I', size=12)
plt.ylabel('V', size=12)
plt.legend(loc='upper left')
plt.savefig('cvcsquid.png')
plt.show()
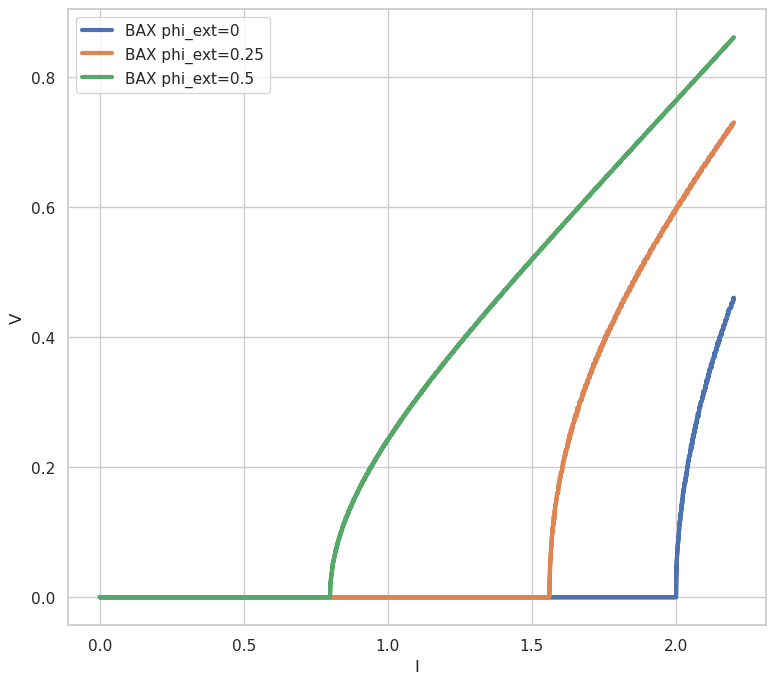
Как видно из графика ВАХ при \(\varphi_{ext}=0\) критический ток равен \(I_{c}=2\), при \(\varphi_{ext}=0.25\) - \(I_{c}=1.58\), а при \(\varphi_{ext}=0.5\) - \(I_{c}=0.8\), т.е. с изменением \(\varphi_{ext}\) меняется величина критического тока.
Исследование зависимости тока возврата от внешнего магнитного поля#
Для этого вводим следующие параметры:
npoint - количество точек в интервале значений внешнего поля
ph_extmin - минимальное значение внешнего поля
ph_extmax - максимальное значение внешнего поля
deltaph_ext - шаг изменения внешнего поля
npoint = 51
ph_extmin = 0.0
ph_extmax = 2.0
deltaph_ext = (ph_extmax - ph_extmin) / (npoint-1)
print(deltaph_ext)
0.04
Создаем массив значений внешнего поля для которых нужно вычислить ток возврата
ph_ext_array = np.linspace(ph_extmin, ph_extmax, num=npoint)
ph_ext_array.shape
(51,)
Создаем пустой массив для значений тока возврата
Ireturn_array = np.zeros(npoint)
Ireturn_array.shape
(51,)
Ток возврата - это ток при которой в ходе уменьшения внешнего тока напряжение приравнивается к нулю.
Поэтому рассчет начинаем от максимального тока (Imax).
Imax = 2.2
@njit
def get_Ireturn(s0, beta_c, beta_L, Pi, n, ph_ext,
nt, ntmin, t0, deltat, deltaI, epsilon):
''' Функция для вычисления значении тока возврата при заданных параметров.
Возвращает для заданного значения параметров значение тока возврата.
s0 - массив начальных условий,
beta_c, beta_L, Pi, n, Icurr, ph_ext,-параметры модели
nt - количество точек по времени, в которых найдены решение,
ntmin - номер шага по времени соответсвующее
нижней границе интегрирования,
t0-начальное значение времени,
deltat - шаг по времени
deltaI - шаг по току
epsilon - точность нахождения тока возврата
'''
Icurr = Imax
a = -1
while Icurr < 100:
res = cvcpoint_new(s0, beta_c, beta_L, Pi, n,
Icurr, ph_ext, nt, ntmin, t0, deltat)
Vav = res[0]
s0 = res[1:]
# print(Icurr)
if (Vav <= epsilon):
Ireturn = Icurr
break
Icurr -= deltaI
return Ireturn
@njit
def funk_numba_return(j, ph_extmin, deltaph_ext, s0, beta_c, beta_L,
Pi, n, ph_ext, nt, ntmin, t0, deltat, deltaI, epsilon):
''' Функция для вычисления значении тока возврата при заданных параметров и
фиксированном значении потока внешнего магнитного поля с номером j
на отрезке [ph_extmin, j*deltaph_ext].
Возвращает для заданного значения ph_ext значение тока возврата.
s0 - массив начальных условий,
beta_c, beta_L, Pi, n, Icurr, ph_ext,-параметры модели
nt - количество точек по времени, в которых найдены решение,
ntmin - номер шага по времени соответсвующее
нижней границе интегрирования,
t0-начальное значение времени,
deltat - шаг по времени
deltaI - шаг по току
epsilon - точность критического тока
'''
ph_ext = ph_extmin + deltaph_ext * j
Ireturn = get_Ireturn(s0, beta_c, beta_L, Pi, n, ph_ext,
nt, ntmin, t0, deltat, deltaI, epsilon)
return Ireturn
epsilon = 0.1
%%time
for i in range(0, npoint):
Ireturn = funk_numba_return(i, ph_extmin, deltaph_ext, s0, beta_c, beta_L, Pi, n, ph_ext,
nt, ntmin, t0, deltat, deltaI, epsilon)
Ireturn_array[i] = Ireturn
CPU times: user 5min 7s, sys: 412 ms, total: 5min 8s
Wall time: 5min 8s
fig = plt.figure(figsize=(6, 6))
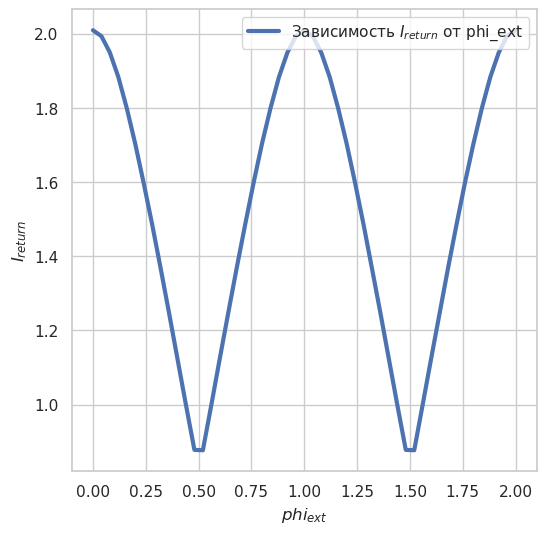
plt.plot(ph_ext_array, Ireturn_array,
label='Зависимость $I_{return}$ от phi_ext', linewidth=3.0)
plt.xlabel('$phi_{ext}$', size=12)
plt.ylabel('$I_{return}$', size=12)
plt.legend(loc='upper right')
plt.savefig('Icfield.png')
plt.show()
4. Вычисление модуляции напряжения при фиксированном токе от внешнего магнитного поля#
npoint - количество точек в интервале значений внешнего поля
ph_extmin - минимальное значение внешнего поля
ph_extmax - максимальное значение внешнего поля
deltaph_ext - шаг изменения внешнего поля
I_curr - значение тока
I_fix_min - минимальное значение тока
I_fix_max - максимальное значение тока
delta_I_fix - шаг на отрезке по току.
n_point - кол-во точек по внешнему полю.
n_fix_point - кол-во точек по току.
ph_ext = 0.0
Icurr = 2.7
n_fix_point = 20
n_point = 300
ph_extmin = 0.0
ph_extmax = 2
delta_ph_ext = (ph_extmax - ph_extmin) / (n_point-1)
I_fix_min = 0.2
delta_I_fix = 0.1
I_fix_max =I_fix_min + n_fix_point *delta_I_fix
I_fix_array - массив точек по току.
ph_ext_array - массив точек по внешнему полю.
I_fix_array = np.linspace(I_fix_min, I_fix_max, num = n_fix_point)
I_fix_array.shape
(100,)
ph_ext_array = np.linspace(ph_extmin, ph_extmax, num=n_point)
ph_ext_array.shape
print(ph_ext_array)
[0. 0.10526316 0.21052632 0.31578947 0.42105263 0.52631579
0.63157895 0.73684211 0.84210526 0.94736842 1.05263158 1.15789474
1.26315789 1.36842105 1.47368421 1.57894737 1.68421053 1.78947368
1.89473684 2. ]
Vmod_array = []
@njit
def get_Vmod(s0, beta_c, beta_L, Pi, n, ph_ext,
nt, ntmin, t0, deltat, deltaI):
''' Функция для вычисления значении критического тока
при заданных параметров. Возвращает для заданного
значения параметров значение критического тока.
s0 - массив начальных условий,
beta_c, beta_L, Pi, n, Icurr, ph_ext,-параметры модели
nt - количество точек по времени, в которых найдены решение,
ntmin - номер шага по времени соответсвующее
нижней границе интегрирования,
t0-начальное значение времени,
deltat - шаг по времени
deltaI - шаг по току
epsilonV - точность нахождения модулированного напряжения
'''
a = 1
res = comput_vax(s0, beta_c, beta_L, Pi, n, Icurr, ph_ext, nt, ntmin, t0, deltat, a, deltaI)
# print(ph_ext)
return res
@njit
def numba_V_mod (j, ph_extmin, deltaph_ext, s0, beta_c, beta_L, Pi, n, ph_ext,
nt, ntmin, t0, deltat, deltaI, I_fix_array, n_fix_point):
''' Функция для вычисления значении модуляции напряжения от величины внешнего поля
при заданных параметров. Возвращает для заданного значения параметров и величин внешнего поля
массивы значений напряжения, извлеченных из соответсВАХ.
s0 - массив начальных условий,
beta_c, beta_L, Pi, n, Icurr, ph_ext,-параметры модели
nt - количество точек по времени, в которых найдены решение,
ntmin - номер шага по времени соответсвующее нижней границе интегрирования,
t0-начальное значение времени,
deltat - шаг по времени
deltaI - шаг по току
'''
V_I = []
ph_ext = ph_extmin + j* deltaph_ext
cvc = get_Vmod(s0, beta_c, beta_L, Pi, n, ph_ext,
nt, ntmin, t0, deltat, deltaI)
cvc_0 = cvc[:, 0]
for i in I_fix_array:
# Находим индекс минимального значения
min_index = np.argmin(np.abs(cvc_0 - i))
V_I.append(cvc[min_index][1])
return V_I
Создаем массив, в который будем заполнять значения напряжений при определенных значений тока.
%%time
Vmod_array = np.empty((n_point, n_fix_point), dtype=np.float64)
for i in range(0, n_point):
Vmod = numba_V_mod(i, ph_extmin, delta_ph_ext, s0, beta_c, beta_L, Pi, n,
ph_ext, nt, ntmin, t0, deltat, deltaI, I_fix_array, n_fix_point)
Vmod_array[i] = Vmod
CPU times: user 4min 19s, sys: 404 ms, total: 4min 19s
Wall time: 4min 19s
Обозначим np.array(Vmod_array) = data и вычислим значение num - кол-во кривых модуляции
data = np.array(Vmod_array)
print(len(data[:,0]))
num = len(data[0])
print(len(ph_ext_array))
20
20
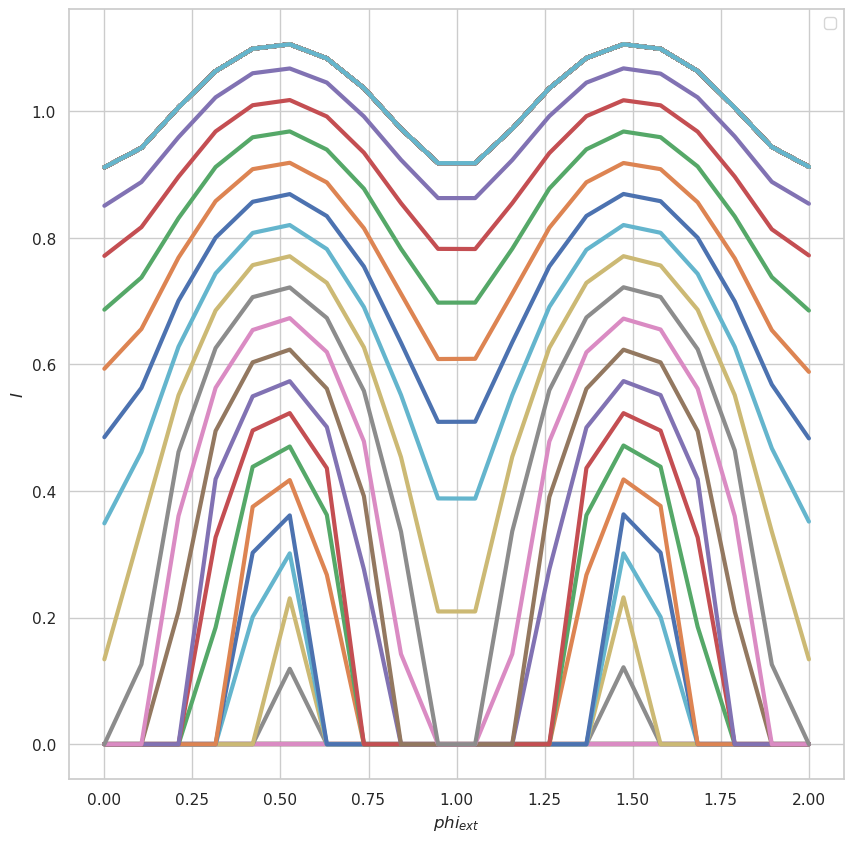
Построим зависимости напряжений от внешнего поля при различных значениях тока
fig = plt.figure(figsize=(10, 10))
for a in range (0, num):
plt.plot(ph_ext_array, data[:, a], linewidth=3.0)
plt.xlabel('$phi_{ext}$', size=12)
plt.ylabel('$I$', size=12)
plt.legend('beta_C = {beta_C}', 'beta_L = {beta_L}')
plt.show()
/tmp/ipykernel_407029/1188417558.py:6: UserWarning: Legend does not support handles for str instances.
A proxy artist may be used instead.
See: https://matplotlib.org/stable/users/explain/axes/legend_guide.html#controlling-the-legend-entries
plt.legend('beta_C = {beta_C}', 'beta_L = {beta_L}')
Параллелизация с numba#
Материалы документации Numba
Setting the Number of Threads
The number of threads used by numba is based on the number of CPU cores available (see numba.config.NUMBA_DEFAULT_NUM_THREADS), but it can be overridden with the NUMBA_NUM_THREADS environment variable.
https://numba.readthedocs.io/en/stable/developer/threading_implementation.html
from numba import config, njit, threading_layer
from numba import set_num_threads, get_num_threads
# set the threading layer before any parallel target compilation
config.THREADING_LAYER = 'threadsafe'
config.NUMBA_DEFAULT_NUM_THREADS
80
config.THREADING_LAYER = 'omp'
import os
print('NUMBA NUM THREADS')
try:
print(os.environ['NUMBA_NUM_THREADS'])
except:
print(config.NUMBA_DEFAULT_NUM_THREADS)
NUMBA NUM THREADS
80
import numba as nb
from numba import prange
Параллелизация вычисления зависимости тока возврата от величины внешнего поля#
npoint = 51
ph_extmin = 0.0
ph_extmax = 2.0
deltaph_ext = (ph_extmax - ph_extmin) / (npoint-1)
print(deltaph_ext)
ph_ext_array = np.linspace(ph_extmin, ph_extmax, num=npoint)
ph_ext_array.shape
0.04
(51,)
@njit(parallel=True)
def comput_parallel_I_return(npoint, ph_extmin, deltaph_ext, s0, beta_c, beta_L, Pi, n,
ph_ext, nt, ntmin, t0, deltat, deltaI, epsilon):
''' Функция для вычисления зависимости тока возврата
от потока внешнего магнитного поля при заданных параметров.
Возвращает массив значений токов возврата для заданного
интервала значений ph_ext.
npoint - количество точек ph_ext в интервале
ph_extmin - начало интервала потока внешнего магнитного поля,
deltaph_ext - шаг потока внешнего магнитного поля,
s0 - массив начальных условий,
beta_c, beta_L, Pi, n, Icurr, ph_ext,-параметры модели
nt - количество точек по времени, в которых найдены решение,
ntmin - номер шага по времени соответсвующее
нижней границе интегрирования,
t0-начальное значение времени,
deltat - шаг по времени
deltaI - шаг по току
epsilon - точность тока возврата
'''
Ireturn_array = np.empty(npoint)
Ireturn_array[:] = 0
for i in nb.prange(npoint):
Ireturn = funk_numba_return(i, ph_extmin, deltaph_ext, s0, beta_c,
beta_L, Pi, n, ph_ext, nt, ntmin, t0, deltat, deltaI, epsilon)
Ireturn_array[i] = Ireturn
return Ireturn_array
%%time
Ireturn_array = comput_parallel_I_return(npoint, ph_extmin, deltaph_ext, s0, beta_c, beta_L, Pi, n, ph_ext, nt, ntmin, t0, deltat, deltaI, epsilon)
CPU times: user 5min 51s, sys: 813 ms, total: 5min 52s
Wall time: 14.1 s
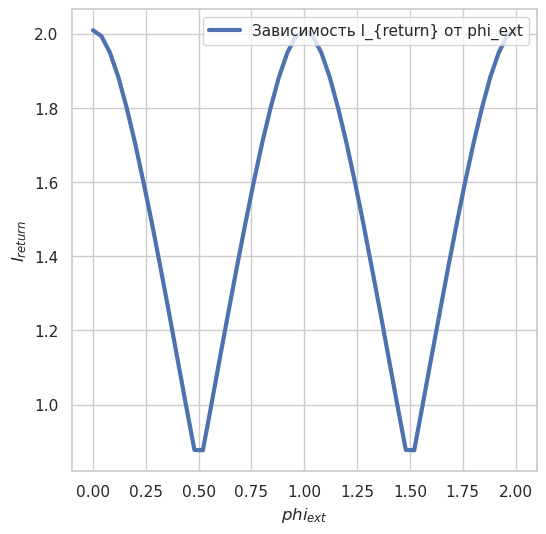
fig = plt.figure(figsize=(6, 6))
plt.plot(ph_ext_array, Ireturn_array,
label='Зависимость I_{return} от phi_ext', linewidth=3.0)
plt.xlabel('$phi_{ext}$', size=12)
plt.ylabel('$I_{return}$', size=12)
plt.legend(loc='upper right')
plt.show()
Параллелизация вычисления зависимости модуляции напряжения от величины внешнего поля#
ph_ext-внешнее поле, ph_ext_min- минимальное значение внешнего поля, ph_extmax - максимальное значение внешнего поля, delta_ph_ext - шаг изменения внешнего поля, I_fix_min - минимальное значение тока для вычисления модуляции напряжения, I_fix_max - максимальное значение тока для вычисления модуляции напряжения, delta_I_fix - шаг изменения тока для вычисления модуляции напряжения. n_point - количество точек по внешнему полю. n_fix_point - количество точек по току.
ph_ext = 0.0
Icurr = 2.7
n_fix_point = 20
n_point = 300
ph_extmin = 0.0
ph_extmax = 2
delta_ph_ext = (ph_extmax - ph_extmin) / (n_point-1)
I_fix_min = 0.2
delta_I_fix = 0.1
I_fix_max =I_fix_min + n_fix_point *delta_I_fix
I_fix_array - массив точек по току.
ph_ext_array - массив точек по внешнему полю.
I_fix_array = np.linspace(I_fix_min, I_fix_max, num = n_fix_point)
I_fix_array.shape
(20,)
ph_ext_array = np.linspace(ph_extmin, ph_extmax, num=n_point)
ph_ext_array.shape
(4,)
Vmod_array = []
@njit(parallel=True)
def comput_parallel_V_mod(n_point, ph_extmin, delta_ph_ext, s0, beta_c, beta_L, Pi, n,
ph_ext, nt, ntmin, t0, deltat, deltaI, I_fix_array, n_fix_point):
''' Функция для вычисления значении модуляции напряжения от величины внешнего поля
при заданных параметров. Возвращает для заданного значения параметров и величин внешнего поля
массивы значений напряжения, извлеченных из соответсВАХ.
s0 - массив начальных условий,
beta_c, beta_L, Pi, n, Icurr, ph_ext,-параметры модели
nt - количество точек по времени, в которых найдены решение,
ntmin - номер шага по времени соответсвующее нижней границе интегрирования,
t0-начальное значение времени,
deltat - шаг по времени
deltaI - шаг по току
'''
Vmod_array = np.empty((n_point, n_fix_point), dtype=np.float64)
# new_arr = []
for i in nb.prange(n_point):
Vmod = numba_V_mod(i, ph_extmin, delta_ph_ext, s0, beta_c, beta_L, Pi, n,
ph_ext, nt, ntmin, t0, deltat, deltaI, I_fix_array, n_fix_point)
Vmod_array[i]=Vmod
return Vmod_array
Создаем массив, в который будем заполнять рассчитанные значений напряжения с изменением внешнего поля.
%%time
Vmod_array = comput_parallel_V_mod(n_point, ph_extmin, delta_ph_ext, s0, beta_c, beta_L, Pi, n, ph_ext, nt, ntmin, t0, deltat, deltaI, I_fix_array, n_fix_point)
CPU times: user 1min 2s, sys: 553 ms, total: 1min 3s
Wall time: 18.7 s
Обозначим np.array(Vmod_array) = data и вычислим значение num - количество кривых модуляции напряжения
print(Vmod_array)
[[ 1.69499714e-12 -1.86973683e-12 5.33284545e-13 -8.31354652e-12
-8.14992602e-13 -2.05586823e-13 -2.68358034e-12 -1.05219235e-11
1.03259674e-11 -5.79752522e-12 -1.67572572e-11 -4.99187715e-12
-1.69603867e-12 -1.45710002e-11 3.72771595e-12 1.22817770e-11
-1.12167560e-11 -3.43144085e-08 3.15166109e-01 4.60495652e-01]
[ 1.34547695e-12 -3.57796643e-12 -7.83029998e-12 2.78705096e-13
-3.30862512e-12 1.48667530e-11 3.89322628e-12 -4.26815458e-12
-3.85719161e-12 -3.52771299e-12 -3.62327779e-11 1.81252656e-01
3.26185752e-01 4.17454839e-01 4.92111290e-01 5.60845840e-01
6.23947085e-01 6.84899670e-01 7.44958889e-01 8.02487914e-01]
[ 4.26700346e-12 -1.34912346e-12 -8.60547155e-12 -7.79911861e-12
2.74682069e-12 5.21910454e-12 7.85144255e-12 -7.10788519e-14
-1.39098533e-11 1.96622643e-11 -6.11951302e-12 1.83864680e-01
3.26210348e-01 4.15999693e-01 4.92004809e-01 5.61114560e-01
6.22873613e-01 6.85952233e-01 7.45231310e-01 8.03268375e-01]
[-2.07231558e-12 1.74848465e-12 -2.98256500e-13 -2.15779507e-12
1.16095386e-11 3.97401380e-13 -1.95437942e-12 5.81752350e-12
-4.71583515e-13 -8.69916250e-12 -2.76726320e-12 5.69774767e-13
-9.18000367e-12 -2.46355351e-11 4.00687426e-12 1.27242513e-11
-1.79850490e-11 -3.39905668e-08 3.10487736e-01 4.56978494e-01]]
data = np.array(Vmod_array)
num = len(data[0])
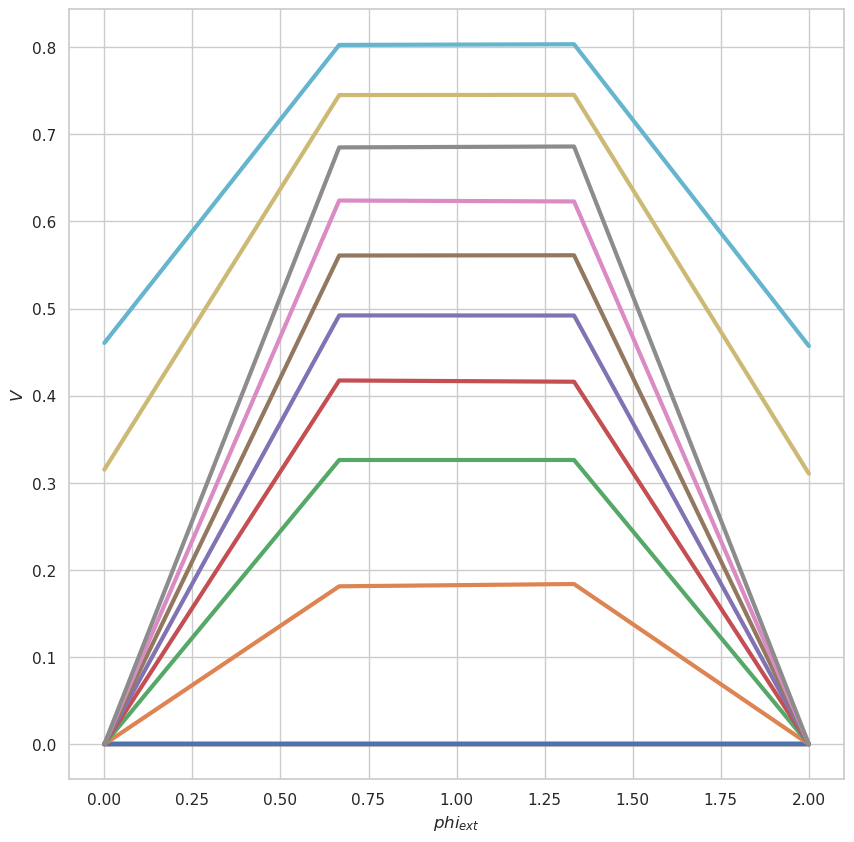
fig = plt.figure(figsize=(10, 10))
for a in range(0, num):
plt.plot(ph_ext_array, data[:, a], label = a, linewidth=3.0)
plt.xlabel('$phi_{ext}$', size=12)
plt.ylabel('$V$', size=12)
plt.show()
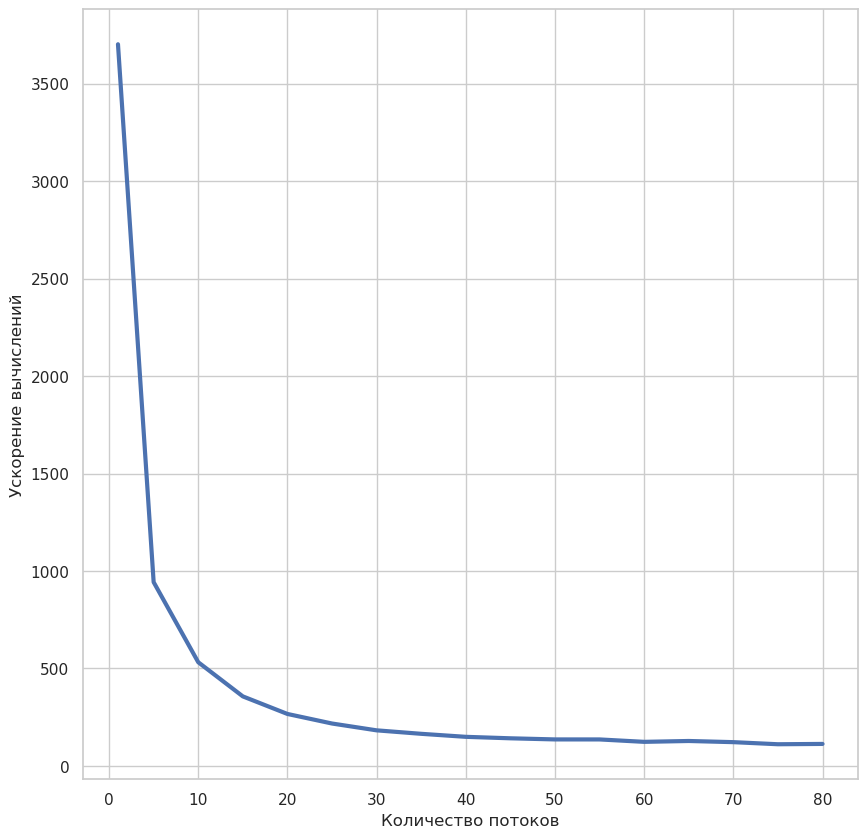
Вычисления при разных чисел потоков.
На этом этапе реализована параллелизация вычислении критического тока. На графике представлена рассчитанная зависимость критического тока СКВИДа от потока \(\varphi_{ext}\) в интервале потока [0, 2]. Данная зависимость демонстрирует модулирование критического тока с изменением \(\varphi_{ext}\), что согласуется с известными результатами. Теперь можно вычислить зависимость времени вычисления от числа вычислительных потоков.
num_treads = [1, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80]
time_stamp = []
for i in num_treads:
set_num_threads(i)
t_start = time.time()
Vmod_array = comput_parallel_V_mod(n_point, ph_extmin, delta_ph_ext, s0, beta_c, beta_L, Pi, n, ph_ext, nt, ntmin, t0, deltat, deltaI, I_fix_array, n_fix_point)
t_finish = time.time()
time_stamp.append(t_finish - t_start)
print(f'Execution time {t_finish - t_start} s')
fig = plt.figure(figsize=(10, 10))
# for a in range (0, len(res)):
plt.plot(num_treads, time_stamp, label = a, linewidth=3.0)
plt.xlabel('$Threads number$', size=12)
plt.ylabel('$Time (s)$', size=12)
plt.savefig('Time_Num_threads.png')
plt.show()
total_time - массив времени расчетов
total_time = [3702.65714263916, 942.7957887649536, 531.9059028625488, 356.6171684265137, 266.47338223457336, 217.4221169948578, 182.3952293395996, 164.5790901184082, 149.1030695438385, 141.55036878585815, 135.79208898544312, 135.71493935585022, 123.3793740272522, 127.7741801738739, 121.7995765209198, 111.03557324409485, 112.71054816246033]
ax = []
for i in time_stamp:
local_ax = time_stamp[0] / i
ax.append(local_ax)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[71], line 1
----> 1 for i in time_stamp:
2 local_ax = time_stamp[0] / i
3 ax.append(local_ax)
NameError: name 'time_stamp' is not defined
fig = plt.figure(figsize=(10, 10))
# for a in range (0, len(res)):
plt.plot(num_treads, ax, label = a, linewidth=3.0)
plt.xlabel('Количество потоков', size=12)
plt.ylabel('Ускорение вычислений', size=12)
plt.savefig('Ax_Num_threads.png')
plt.show()