Python-инструментарий для моделирования динамики джозефсоновского перехода под воздействием внешнего излучения#
В блокноте представлен инструментарий для моделирования динамики джозефсоновского перехода под воздействием внешнего излучения:
алгоритм для вычисления вольт-амперной характеристики джозефсоновского перехода под воздействием внешнего излучения;
алгоритм вычисления зависимости ширины ступеньки Шапиро от амплитуды;
алгоритм параллельного вычисления зависимости ширины ступеньки Шапиро от амплитуды с использованием библиотеки Joblib;
результаты анализа эффективности параллельных вычислений.
Исследование основано на материалах статей:
Josephson B.D. Possible new effects in superconductive tunnelling // Physics Letters - 1962. - V. 1, no. 7. - P. 251-253.
Shapiro S. Josephson currents in superconducting tunneling: The effect of microwavesand other observations // Phys. Rev. Lett. - 1963. - V. 11, no. 2. - P.80-82.
McCumber D.E. Effect of ac Impedance on dc Voltage-Current Characteristics of Superconductor Weak-Link Junctions // Journal of Applied Physics - 1968. - V. 39, no. 7. - P.3113-3118.
1. Описание модели#
Эффект Джозефсона и джозефсоновский переход
Связь двух сверхпроводящих слоев посредством тонкого слоя несверхпроводящего барьера образует структуру называемую джозефсоновским переходом (в честь английского ученого Брайана Джозефсона). При пропускании электрического тока через джозефсоновский переход (ДП) в зависимости от величины тока наблюдается стационарный и нестационарный эффект Джозефсона.
Стационарный эффект Джозефсона. При пропускании тока ниже критического значения \((I<I_{c})\) в ДП отсутствует напряжение и через переход течет сверхпроводящий ток. Данный ток пропорционален синусу разности фаз параметров порядка сверхпроводящих слоев образующих ДП:
\( \begin{eqnarray} I_{s}=I_{c}\sin\varphi. \label{eq1} \tag{1} \end{eqnarray} \)
Нестационарный эффект Джозефсона. При увеличении тока выше критического значения \((I>I_{c})\) возникает переменное напряжение в ДП и оно пропорционально производной разности фаз
\( \begin{eqnarray} V=\frac{\hbar}{2e}\frac{d\varphi}{dt}. \label{eq2} \tag{2} \end{eqnarray} \)
Система уравнений для описания динамики ДП:
Динамика ДП описывается в рамках RCSJ-модели (Resitively Capasitevily Shunted Junction) [3]. В рамках этой модели ДП моделируется как параллельное соединение конденсатора, резистора и сверхпроводника:
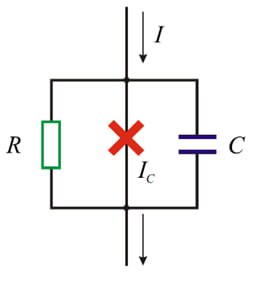
Через конденсатор течет ток смещения \(\displaystyle I_{disp}=C\frac{dV}{dt}\), через резистор - квазичастичный ток \(\displaystyle I_{qp}=\frac{V}{R}\) и через сверхпроводник джозефсоновский (сверхпроводящий) ток \(I_{s}=I_{c}\sin\varphi\).
Полный ток, проходящий через систему, равен сумме вышеперечисленных токов
\( \begin{eqnarray} I=C\frac{dV}{dt}+\frac{V}{R}+I_{c}\sin\varphi. \label{eq3} \tag{3} \end{eqnarray} \)
Используя (2) и (3) в нормированных величинах можно написать замкнутую систему дифференциальных уравнений относительно \(V\) и \(\varphi\)
\( \begin{eqnarray} \begin{cases} \displaystyle \frac{dV}{dt} = I-\beta V-\sin\varphi,\\ \displaystyle \frac{d\varphi}{dt}=V, \end{cases} \label{eq4} \tag{4} \end{eqnarray} \)
где \(\displaystyle \beta=\frac{\hbar \omega_{p}}{2 e I_{c}R}\) - параметр диссипации, \(\displaystyle\omega_{p}=\sqrt{\frac{2 e I_{c}}{\hbar C}}\) - плазменная частота. В системе уравнений (\ref{eq4}) время нормирован на \(\omega_{p}\), напряжение нормировано на \(\displaystyle V_{0}=\frac{\hbar \omega_{p}}{2 e}\) и ток нормирован на \(I_{c}\).
Влияние внешнего излучения на динамику ДП и ступеньки Шапиро
Под воздействием внешнего излучения, при условии кратности частоты Джозефсона к частоте внешнего излучения, в результате частотного захвата через ДП возникает не зависящий от времени сверпроводящий ток. Этот сверхпроводящий ток на вольт-амперной характеристике (ВАХ) проявляется в виде ступеньки постоянного напряжения, называемой ступенькой Шапиро [2]. Ширина ступеньки Шапиро зависит от величины частоты и амплитуды внешнего излучения.
Для моделирования этого явления в системе уравнений RCSJ-модели учитывается дополнительный переменный ток \(I_{R}\), создаваемый внешним излучением с амплитудой \(A\) и частотой \(\omega\), т.е. \(I_{R}=A\sin(\omega t)\).
Алгоритм проведения расчетов основан на решении системы уравнений при фиксированном значении тока с выбранным шагом. Отметим, что, при решении системы уравнений для каждого значения тока, время меняется от нуля до \(T_{\max}\). В этом случае, если уравнения зависят в явном виде от времени, то возникает необходимость организовать изменения времени непрерывно во всем интервалам по току. Для этого нужно будет считать количество шагов по току и умножать на \(T_{\max}\) и прибавить к текущему значению времени. Эту сложность можно нивелировать, добавив к системе уравнений дополнительное уравнение типа \(du/dt=\omega\). Тогда на следующий шаг по току необходимо только передавать начальное условие, что упрощает процесс вычислений.
Таким образом конечный вид системы уравнений принимает вид:
\( \begin{eqnarray} \begin{cases} \displaystyle \frac{dV}{dt} = I+A\sin(u)-\beta V-\sin\varphi,\\ \displaystyle \frac{d\varphi}{dt}=V,\\ \displaystyle \frac{du}{dt}=\omega. \end{cases} \label{eq5} \tag{5} \end{eqnarray} \)
Параметры модели:
\(\beta\) - параметр диссипации;
\(A\) - амплитуда внешнего излучения;
\(V\) - напряжение;
\(I\) - внешний ток;
\(\omega\) - частота излучения;
\(\varphi\) - разность фаз.
Постановка задачи:
Вычислить вольт-амперную характеристику джозефсоновского перехода под воздействием внешнего излучения и построить ее график.
2. Вычисление вольт-амперной характеристики#
Алгоритм вычисления вольт-амперной характеристики:
Задаем значения параметров модели, параметры численного счета, начальные условия.
Численно решаем задачу Коши для системы обыкновенных дифференциальных уравнений (5), (например, методом Рунге-Кутта четвертого порядка) для фиксированного значения тока \(I\), и находим временную зависимость разности фаз \(\varphi(t)\) и напряжения \(V(t)\).
Усредняем полученную зависимость \(V(t)\) по времени:
\( \displaystyle <V>=\frac{1}{T_{\max}-T_{\min}}\int\limits_{T_{\min}}^{T_{\max}}V(t)dt \)
В результате получим значение напряжения для заданного значения тока, т.е. определяем одну точку на ВАХ.
Меняем значение тока на \(\delta I\) и повторяем п. 2, используя при этом \(\varphi(T_{\max})\) и \(V(T_{\max})\) из посчитанного значения тока в качестве начального условия, и для полученного \(V(t)\) выполняем п. 3, и находим среднее значение напряжения.
Проводим расчеты до \(I_{\max}\).
Проводим расчеты, уменьшая значение тока \(I\) от \(I_{\max}\) до нуля.
Теперь, непостредственно переходим к реализации вышеописанного алгоритма.
Подключаем библиотеки
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from functools import partial
from scipy.integrate import odeint
import time
import seaborn as sns
sns.set()
sns.set(style="whitegrid")
%matplotlib inline
Определяем правые части уравнений
# Функция, определяющая правую часть систему уравнений
def shortjj(t, S, beta, Iext, A, omega):
''' Определяет правые части системы ОДУ (5),
beta, A, omega - параметры модели,
S=[phi,V,u] - искомое решение '''
ph = S[0]
V = S[1]
u = S[2]
dph = V
dV = Iext - np.sin(ph) - beta * V + A * np.sin(u)
du = omega
dS = [dph, dV, du]
return dS
Вычисления временной зависимости напряжения#
Зададим функцию для вычисления временной зависимости напряжение и фазы при фиксированном значении внешнего тока, которая используя начальные условия, значения параметров модели и численного счета, возвращает соответствующие временные зависимости.
Задаем функцию для численного решения задачи Коши
def jjsolution(s0, Iext, beta, A, omega, nt, t0, deltat):
''' Численное решение задачи Коши для системы ОДУ (5),
beta, A, omega - параметры модели,
nt - количество точек по времени, в которых находится решение,
t0 - начальное значение времени,
deltat - шаг по времени,
Iext - значение внешнего тока,
s0=[phi0, V0, u0] - начальные условия,
output: [phtime, Vtime, utime] - массивы посчитанных временных зависимостей для фазы, напряжения и введенной вспомогательной функции u '''
f = partial(shortjj, beta=beta, Iext=Iext, A=A, omega=omega)
t_e = np.linspace(t0, nt*deltat, nt)
sol_1 = solve_ivp(f, [t0, nt*deltat], s0, t_eval=t_e, method='RK45',
rtol=1e-8, atol=1e-8)
phtime = sol_1.y[0]
Vtime = sol_1.y[1]
utime = sol_1.y[2]
return [phtime, Vtime, utime]
Для проверки корректности реализованной вычислительной схемы найдем временные зависимости напряжения в двух режимах:
в состоянии с нулевым средним напряжением,
в состоянии с конечным средним напряжением.
Согласно физики джозефсоновского перехода, в качестве результата мы должны получить в первом случае - затухающую зависимость напряжения от времени, а во втором - осцилляцию напряжения с конечным средним значением. Для этого необходимо выбрать значения тока при котором реализации таких решений возможно (например \(I=0.4\)) и нужно решить систему уравнений с разными начальными условиями для напряжения (например, \(V=3\)). Для простоты рассмотрим случай без внешнего излучения, т.е. \(A=0\).
Параметры модели
beta = 0.2 # Параметр диссипации
A = 0 # Амплитуда внешнего излучения
omega = 2 # Частота внешнего излучения
Параметры численного счета
Tmax = 100 # Максимальное значение времени
deltat = 0.05 # шаг по времени
t0 = 0
nt = int(Tmax/deltat)
1. Решение для состояния с нулевым средним напряжением#
Iext = 0.4 # Значение внешнего тока
V0 = 0 # Значение напряжение в начальный момент времени
time_array = np.linspace(0, Tmax, num=nt)
s0 = np.array([0, V0, 0])
res = jjsolution(s0, Iext, beta, A, omega, nt, t0, deltat)
Vtime = res[1]
Построим график временной зависимости \(V(t)\)
fig = plt.figure(figsize=(8, 6))
plt.plot(time_array, Vtime, label='Time dependence', linewidth=3.0)
plt.xlabel('Time', size=12)
plt.ylabel('V', size=12)
plt.legend(loc='upper right')
plt.show()
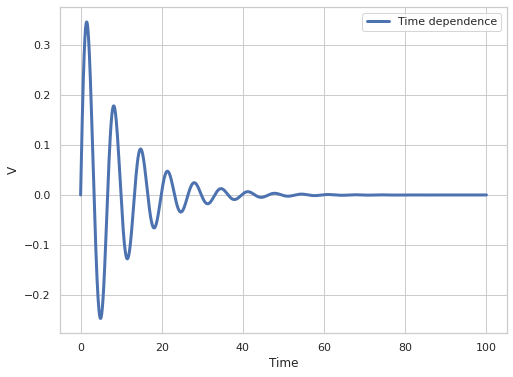
Рис. 1. График зависимости напряжения от времени с нулевым средним напряжением
Для сохранения полученных графиков можно использовать метод библиотеки Matplotlib:
fig.savefig('Vtime1.png')
Для сохранения результатов расчетов в файл можно использовать метод библиотеки NumPy:
time_dep = np.column_stack((time_array, Vtime))
np.savetxt('Vtime1.dat', time_dep)
Как отмечалось выше, согласно физике ДП, значение напряжения должно стремиться к нулю. Как видно из Рис. 1, в начале интервала интегрирования значение напряжения, осцилируя, стремится к нулю и стабилизируется начиная от времени \(T_{min}=60\). Поэтому далее при усреднении необходимо это учитывать, т.е. нужно вычислять среднее после стабилизации решения.
2. Решение для состояния с конечным средним напряжением#
Iext = 0.4 # Значение внешнего тока
V0 = 3 # Значение напряжение в начальный момент времени
time_array = np.linspace(0, Tmax, num=nt)
s0 = np.array([0, V0, 0])
res = jjsolution(s0, Iext, beta, A, omega, nt, t0, deltat)
Vtime = res[1]
Построим график временной зависимости \(V(t)\)
fig = plt.figure(figsize=(8, 6))
plt.plot(time_array, Vtime, label='Time dependence', linewidth=3.0)
plt.xlabel('Time', size=12)
plt.ylabel('V', size=12)
plt.legend(loc='upper right')
plt.show()
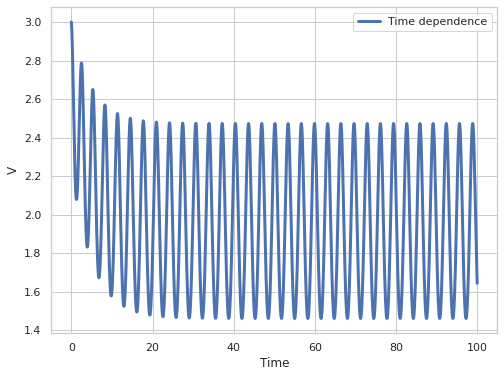
Рис. 2. График зависимости напряжения от времени с конечным средним напряжением
На данном этапе реализован п. 2 алгоритма вычисления ВАХ. Определим функцию для усреднения напряжения \(V(t)\) и вычисления одной точки ВАХ.
Усредняем посчитанные значения напряжения при заданном значении внешнего тока#
Задаем функцию для усреднения временной зависимости напряжения
def averageV(ntmin, nt, deltat, V):
intV = 0
for i in range(ntmin, nt):
intV += V[i]*deltat
Vav = intV/((nt-ntmin)*deltat)
return Vav
Задаем функцию для вычисления одной точки ВАХ
def cvcpoint(s0, Iext, beta, A, omega, nt, t0, ntmin, deltat):
solution = jjsolution(s0, Iext, beta, A, omega, nt, t0, deltat)
phtime = solution[0]
Vtime = solution[1]
utime = solution[2]
s0 = np.array([phtime[nt-1], Vtime[nt-1], utime[nt-1]])
Vav = averageV(ntmin, nt, deltat, Vtime)
return [Vav, s0]
Вычисляем ВАХ#
Задаем значения параметров для вычисления ВАХ
Отметим, что при вычислении необходимо согласовать все временных характеристики с периодом внешнего излучения во избежании накоплении ошибок при усреднении. Для этого нужно вычислить период внешнего излучения \(T=2\pi/\omega\). Из построенных выше графиков видно, что решения стабилизируется после \(T_{\min}=60\) (для \(\omega=2\)), это соответствует примерно \(T_{\min}=20T\) (начало интервала для усреднения). Для вычисления ВАХ если выберем временной интервал \(T_{\max}=250\) это будет соответствовать примерно \(T_{\max} = 80T\) (максимальное значение времени) и, соответственно, шаг по времени \(\Delta t=T/50\).
T = 2 * np.pi/omega # Период внешнего излучение
Tmin = 20 * T # Начало интервала для интегрирования для усреднения
Tmax = 80 * T # Максимальное значение времени
deltat = T/50 # шаг по времени
ntmin = int(Tmin/deltat)
nt = int(Tmax/deltat)
deltaIext = 0.01
Iext = 0.0
a = 1.0
Iext_max = 1.2
A = 0.5
Vplot = []
Iplot = []
s0 = np.array([0, 0, 0])
Введем параметр Ilimit, ограничивающий интервал изменеия по току для избежания зацикливания расчета.
Ilimit = 100
t_start = time.time()
while Iext < Ilimit:
res = cvcpoint(s0, Iext, beta, A, omega, nt, t0, ntmin, deltat)
Vav = res[0]
s0 = res[1]
Vplot.append(Vav)
Iplot.append(Iext)
Iext += a * deltaIext
if(Iext > Iext_max):
a = - 1
if ((Iext < 0) and (a == - 1)):
break
t_finish = time.time()
print(f'Execution time {t_finish - t_start} s')
Execution time 69.81972432136536 s
Построим график ВАХ#
fig = plt.figure(figsize=(8, 6))
plt.plot(Iplot, Vplot, label='CVC', linewidth=3.0)
plt.xlabel('I', size=12)
plt.ylabel('V', size=12)
plt.legend(loc='upper left')
plt.show()
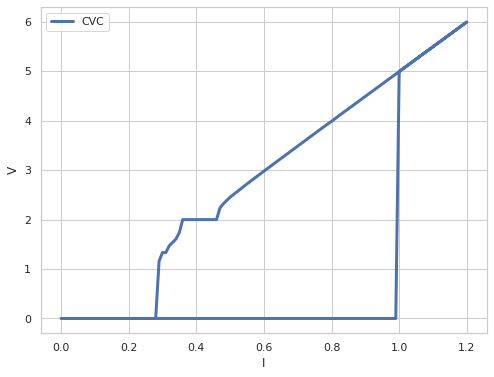
Рис. 3. График ВАХ при значении внешнего излучения \(A=0.5\)
Как видно из Рис. 3 на ВАХ при частоте \(\omega=V=2\) образовалась ступенька постоянного напряжения, т.е. ступенька Шапиро. Для сравнения можно вычислить ВАХ при \(A=0\), т.е. без внешнего излучения и убедится в отсутствии ступеньки.
Для дальнейшего сравнения сохраним рассчитанные занчения ВАХ с внешним излучением в массивах Iplotrad и Vplotrad.
Iplotrad = Iplot
Vplotrad = Vplot
Вычисления ВАХ без внешнего излучения \((A=0)\)#
A = 0
a = 1
Iext = 0.0
s0 = np.array([0, 0, 0])
Vplot = []
Iplot = []
t_start = time.time()
while Iext < Ilimit:
res = cvcpoint(s0, Iext, beta, A, omega, nt, t0, ntmin, deltat)
Vav = res[0]
s0 = res[1]
Vplot.append(Vav)
Iplot.append(Iext)
Iext += a * deltaIext
if(Iext > Iext_max):
a = - 1
if ((Iext < 0) and (a == - 1)):
break
t_finish = time.time()
print(f'Execution time {t_finish - t_start} s')
Execution time 41.52426719665527 s
Построим графики ВАХ с внешним излучением без внешнего излучения
fig = plt.figure(figsize=(8, 6))
plt.plot(Iplotrad, Vplotrad, label='CVC with radiation', linewidth=3.0)
plt.plot(Iplot, Vplot, label='CVC without radiation', linewidth=3.0)
plt.xlabel('I', size=12)
plt.ylabel('V', size=12)
plt.legend(loc='upper left')
plt.show()
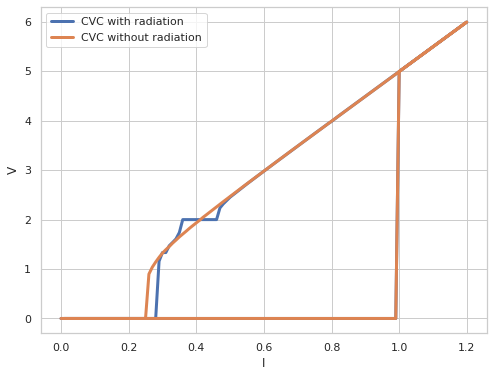
Рис. 4. Графики ВАХ с внешним излучением (\(A=0.5\)) и без внешнего излучения
3. Вычисление зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения#
Алгоритм вычисления зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения#
Задаем значения параметров
Вычислим ВАХ при фиксированном значении амплитуды внешнего излучения. В процессе вычисления сохраняем все значения тока для которых выполняется условия \(V=n_{harm}\omega\) с точностью \(\varepsilon\) (\(\varepsilon>|V-n_{harm}\omega|\)) и как разность максимального и минимального значений из полученных значений тока определяем ширины ступеньки Шапиро. Здесь \(n_{harm}\) обозначает номер гармоники.
Затем увеличивая значение амплитуды на \(\Delta A\) повторяем п.2
Для выполнения п.2 зададим функцию, которая вычисляет ВАХ и ширину ступеньки Шапиро.
Вычисления зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения#
Зададимфункцию для вычисления ВАХ и нахождения ширины ступеньки Шапиро
def Shapirostepsize(A, omega, n_harm, epsilon, Ilimit,
beta, deltaIext, ntmin, nt, deltat):
a = 1
t0 = 0
Iext = 0
Istep_list = []
s0 = np.array([0, 0, 0])
getstep = False # Переменная для проверки попадание на ступеньку
while Iext < Ilimit:
res = cvcpoint(s0, Iext, beta, A, omega, nt, t0, ntmin, deltat)
Vav = res[0]
s0 = res[1]
# Условие для поворота направления тока при первом попадании на ступеньку
# Необходимо для полного получения ступеньки
if ((a == -1) and (getstep == False) and np.abs(Vav-(n_harm*omega)) < epsilon):
a = 1
getstep = True
if ( (a==1) and (getstep==False) and np.abs(Vav-(n_harm*omega))<epsilon):
getstep=True
#Алгоритм определения максимального и минимального значения тока при попадании на ступеньку
if(np.abs(Vav-(n_harm*omega))<epsilon):
Istep_list.append(Iext)
Iext+=a * deltaIext
#Условие изменении направлении тока при выходе из ступеньки
if(Vav>n_harm*omega+0.05):
a=-1
#Условие для остановки цикла по току
if (Vav<n_harm*omega-0.05 and a==-1):
break
#Конец цикла по току
#Вычисление ширины ступеньки
Istep = max(Istep_list)-min(Istep_list)
return Istep
Вычислим ширину ступеньки Шапиро для \(n_{harm}=1\) и \(A=1\) с точностью \(\varepsilon=0.01\)
A = 1
n_harm = 1
epsilon = 0.01
t_start = time.time()
k = Shapirostepsize(A, omega, n_harm, epsilon, Ilimit,
beta, deltaIext, ntmin, nt, deltat)
t_finish = time.time()
print(f'Execution time {t_finish - t_start} s')
print(k)
Execution time 55.185770988464355 s
0.2300000000000002
Последовательное вычисление зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения#
Вводим параметры для вычисления зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения
npoint - количество точек в интервале значений амлитуды;
Amin - минимальное значение амлитуды;
Amax - максимальное значение амплитуды;
deltaA - шаг изменения амплитуды.
npoint = 160
Amin = 0.5
Amax = 40
deltaA = (Amax - Amin) / (npoint-1)
print(deltaA)
0.24842767295597484
Создаем массив значений амплитуды, для которых нужно вычислить ширины ступеньки Шапиро
A_array = np.linspace(Amin, Amax, num=npoint)
Создаем пустой массив для значений ширины ступеньки Шапиро
Step_array = np.zeros(npoint)
Создаем функцию для вычисления зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения
def funk_ShapiroA(j, A, omega, n_harm, epsilon, Ilimit,
beta, deltaIext, ntmin, nt, deltat):
A = Amin + deltaA * j
step = Shapirostepsize(A, omega, n_harm, epsilon, Ilimit,
beta, deltaIext, ntmin, nt, deltat)
return step
Вычислим зависимости ширины ступеньки Шапиро от амплитуды в последовательном режиме#
%%time
for i in range(0, npoint):
Shapirostep = funk_ShapiroA(i, A, omega, n_harm, epsilon, Ilimit,
beta, deltaIext, ntmin, nt, deltat)
Step_array[i] = Shapirostep
CPU times: user 1h 38min 42s, sys: 1.86 s, total: 1h 38min 44s
Wall time: 1h 38min 56s
Построим график зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения#
fig = plt.figure(figsize=(8, 6))
plt.plot(A_array, Step_array, label='Shapiro step width', linewidth=3.0)
plt.xlabel('A', size=12)
plt.ylabel('Stepwidth', size=12)
plt.legend(loc='upper right')
plt.show()
Рис. 5. График зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения
Расчет занимает продолжительное время, поэтому проведем расчеты в параллельном режиме.
Параллельная реализация вычислительной схемы нахождения зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения#
Проведение расчетов в параллельном режиме с использованием библиотеки Joblib
Для распараллеливания вычислений по параметру \(V\) используем функционал библиотеки Joblib, которая позволяет с помощью метода Parallel распределить вычисления по заданному количеству физических ядер процесоров n_jobs. Подробное описание возможностей библиотеки представленно в отдельном разделе HLIT Jbook.
Подключаем необходимые библиотеки для параллельного вычисления#
import joblib
from joblib import Parallel, delayed
import time
import os
print(f"Number of cpu: {joblib.cpu_count()}")
Number of cpu: 80
Вычислим зависимость ширины ступеньки Шапиро от амплитуды внешнего излучения в параллельном режиме
def funk_parallel(j, A, omega, n_harm, epsilon, Ilimit,
beta, deltaIext, ntmin, nt, deltat):
A = Amin + deltaA * j
step = Shapirostepsize(A, omega, n_harm, epsilon, Ilimit,
beta, deltaIext, ntmin, nt, deltat)
return step
t_start = time.time()
rez = Parallel(n_jobs=20)(delayed(funk_parallel)(i, A, omega, n_harm, epsilon, Ilimit,
beta, deltaIext, ntmin, nt, deltat) for i in range(npoint))
t_finish = time.time()
print(f'Execution time {t_finish - t_start} s')
Execution time 323.6772277355194 s
Step_array_parr = np.array(rez)
fig = plt.figure(figsize=(8, 6))
plt.plot(A_array, Step_array_parr, label='Shapiro step width',
linewidth=3.0)
plt.xlabel('A', size=12)
plt.ylabel('Stepwidth', size=12)
plt.legend(loc='upper right')
plt.show()
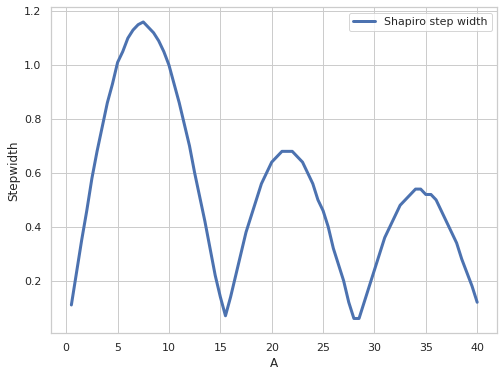
Рис. 6. График зависимости ширины ступеньки Шапиро от амплитуды внешнего излучения
